시간복잡도(time complexity)는 어떻게 계산하는가?

코딩테스트를 준비하면서 어렵다고 느낀 부분은 효율성 검증에서 막혀 통과가 되지 않을때였습니다. 그럴때 고려해야 하는 것이 시간복잡도(time complexity)입니다. 이번 포스팅에서는 시간복잡도에 대해서 알아보고자 합니다.

📝시간복잡도(time complexity)란?

우리가 현실에서 사용하는 컴퓨터는 1초에 32억 번 정도의 연산이 가능하다고 합니다. 실제 코딩테스트에서는 일반적으로 1초당 1억 번의 연산이 가능하다고 생각하고 문제를 풀어야 한다.

• 1부터 n까지 더하는 연산을 프로그래밍한다고 생각해봅니다. 다음 두 가지 방법으로 연산을 진행 할 수 있습니다.

  • 1 + 2 + 3 + … + n
  • (n + 1)*n/2 (가우스 공식)

  첫번째 방법으로 연산을 수행했을 경우 총 n번의 +연산을 수행해야 하지만, 가우스 공식을 수행했을 경우엔 *, +, / 총 3번의 연산만 수행하면 됩니다.

같은 목적의 프로그램을 만들어야 하는 상황에서 보다 더 빨리 실행이 가능한 프로그램을 만들기 위해 시간복잡도(time complexity)를 계산하는 것이 필수적입니다.

시간복잡도 Big-O 표현법

알고리즘에서 시간복잡도는 함수의 입력 값이 n일 때 총 연산횟수인 출력은 대문자 O를 이용하여 표현합니다. 이를 시간복잡도 Big-O 표현법이라고 합니다. 다음은 그 종류입니다.

• 입력값이 n이고 총연산횟수가 n!번 연산일 때 O(n!)
• 입력값이 n이고 총연산횟수가 2ⁿ번 연산일 때 O(2ⁿ)
• 입력값이 n이고 총연산횟수가 n²번 연산은 O(n²)
• 입력값이 n이고 총연산횟수가 n번 연산은 O(n)
• 입력값이 n이고 총연산횟수가 logⁿ번 연산은 O(logⁿ) (logⁿ은 지수가 10인 로그값)
• 입력값 n에 상관없이 총연산횟수가 상수(그 값이 변하지 않는 불변량)번 연산은 O(1)

시간복잡도가 O(n)인 경우

입력값 n에 따라 최악의 경우 n번의 연산을 해야하는 경우 시간복잡도O(n)으로 나타냅니다.

다음 시간복잡도 O(n) 를 예를 들어 설명해보겠습니다.

• 집합의 크기가 10이고 집합에 들어있는 수가 {3, 1, 4, 2, 7, 6, 9, 8, 10} 입니다. 이 때, 찾고자 하는 수 x를 집합의 왼쪽부터 오른쪽 순으로 하나하나 비교하면 몇번 걸리는 지를 봅니다.

  

  찾고자 하는 수 x가 3일 때, 3은 맨 왼쪽에 있으므로 1 번 만에 찾을 수 있다.

  찾고자 하는 수 x가 5일 때, 5는 왼쪽에서 7번째에 있으므로 7번 만에 찾을 수 있다.

  찾고자 하는 수 x가 10일 때, 10은 왼쪽에서 10번째에 있으므로 10번 만에 찾을 수 있다.

집합에서 찾을 수 x를 가장 빨리 찾는 경우는 1번만 찾는 것이고 가장 늦게 찾는 경우는 집합 크기인 10번만에 찾는 것입니다.

위의 예시를 일반화 해보면 집합의 크기가 n일 경우 집합에서 x가 있는지 확인하기 위해서는 1번만에 찾아내는 경우에서 n번 만에 찾아 내는 경우까지가 될 것입니다. 이처럼 최악의 경우 n번의 연산을 해야하는 경우를 시간복잡도 O(n)이라 할수 있습니다.

시간복잡도가 O(logⁿ)인 경우

n값에 따라서 최악의 경우 logⁿ번의 연산을 해야 하는 경우 시간복잡도 O(logⁿ)으로 나타냅니다.

시간복잡도 O(logⁿ)을 알아보기 위해 먼저 로그(log) 계산법을 알아봅시다.

\(log_a b\\ a : 밑 , \; b : 진수\) log의 계산은 밑(a)과 진수(b)에 숫자를 대입하여 결괏값을 얻는 방법입니다. log 식의 계산은 다음과 같습니다.

\[1)\quad log_a 1=0,log_a a=1 \\ 2)\quad log_a M + log_a N = log_a MN\\ 3)\quad log_a M - log_a N = log_a \frac{M}{N}\\ 4)\quad log_a M^k = klog_a M\]

시간복잡도 O(logⁿ)를 계산하는데 필요한 로그 계산법은 위의 공식 중에 1번과 4번 입니다. \(log_2 2 = 1, \; log_2 2^2 = 2, \; log_2 2^{1000} = 1000\\ log_{10} 10 = 1, \; log_{10} 10^5 = 5, \; log_{10} 10^{30000} =30000\) log의 밑과 진수가 같으면 1이 됩니다.

log₄4⁵에서 log의 지수가 4⁵이고 밑이 4라면 진수의 제곱 부분인 5를 앞으로 빼내어 5*log₄4가 되며 이는 5가 됩니다.

log는 직관적으로 이해하기 어렵습니다. 쉽게 생각하면 log₂8 = log₂2³ = 3의 경우, 진수인 8은 밑인 2를 1에 몇 번 곱하면 1 * 2 * 2 * 2 = 8이 되며 총 3번을 곱한 것을 볼 수 있습니다.

log₂10 = 3.32193의 경우, 진수인 10을 밑인 2를 1에 몇 번 곱하면 10이 되는 지 본다면 1에 2를 3.32193곱하면 10이 됩니다.

O(n)을 설명할 때 집합 {3, 1, 4, 2, 7, 6, 5, 9, 8, 10}을 크기가 작은 수가 왼쪽으로 오게 하여 왼쪽에서부터 오른쪽까지 오름차순으로 수를 정렬하면 집합은 {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}이 됩니다.

이 수들을 자신보다 작은 수는 왼쪽 아래로, 자신보다 큰 수를 오른쪽 아래로 두며 자신의 아래에는 최대 2개의 수가 올수 있습니다. 이 모양을 트리라고 하며 트리와 비슷한 행태를 두어 표현하면 아래 그림과 같아집니다.

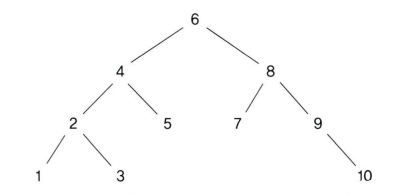
그림 2-2 트리 형태로 배열한 모습

이때 찾고자 하는 수가 x가 있을 때 찾는 방법은 다음과 같은 방법을 이용합니다.

1. 트리의 가장 위(그림상에서 6)를 현재 위치로 둔다.
2. 현재 위치 값과 x가 같다면 종료한다.
3. 다음 중 한가지로 선택
   • 찾고자 하는 수 x가 현재 위치 값보다 작다면 현재 위치를 왼쪽 아래로 옮긴다. -> 2로 이동한다.
   • 찾고자 하는 수 x가 현재 위치 값보다 크다면 현재 위치를 오른쪽 아래로 옮긴다. -> 2로 이동한다.

예를 들어 찾고자 하는 수 x가 6일 때

1. 찾고자 하는 수 6과 현재 위치 값은 6과 같기 때문에 1번 만에 찾을 수 없다.

찾고자 하는 수 x가 5일 때

1. 찾고자 하는 수 5는 현재 위치 값 6보다 작으므로 왼쪽 아래로 현재 위치를 바꾼다.
   • 이 경우 7, 8, 9, 10은 확인해 볼 필요가 없다.
2. 찾고자 하는 수 5는 현재 위치 값 4보다 크므로 오른쪽 아래로 현재 위치를 바꾼다.
   • 이 경우 1, 2, 3은 확인해볼 필요가 없다.
3. 찾고자 하는 수 5와 현재 위치 값 5는 같기 때문에 3번 만에 찾을 수 있다.

찾고자 하는 수 x가 10일때

1. 찾고자 하는 수 10은 현재 위치 값 6보다 크므로 오른쪽 아래로 현재 위치를 바꾼다.
   • 이 경우 1, 2, 3, 4, 5는 확인해볼 필요가 없다.
2. 찾고자 하는 수 10은 현재 위치 값 8보다 크므로 오른쪽 아래로 현재 위치를 바꾼다.
   • 이 경우 7은 확인해볼 필요가 없다.
3. 찾고자 하는 수 10은 현재 위치 값 9보다 크므로 오른쪽 아래로 현재 위치를 바꾼다.
   • 이 경우 8은 확인해볼 필요가 없다.
4. 찾고자 하는 수 10은 현재 위치 값 10과 같기 때문에 4번 만에 찾을 수 있다.

이러한 방식을 이분탐색이라고 합니다. 수가 오름차순 혹은 내림차순으로 정렬되어 있을 때 사용 가능한 탐색방법입니다. 이분탐색은 한 번의 탐색마다 탐색해야 할 수가 2분의 1씩 줄어드는 특징을 볼 수 있습니다. 만약 오른쪽 아래로 현재 위치를 바꾼다면 찾고자 하는 수는 왼쪽 아래 부분보다는 무조건 크다는 것을 보장하므로 왼쪽 아래 부분은 탐색할 필요가 없기 때문입니다.

집합에서 찾을 수 x를 가장 빨리 찾는 경우는 1번 만에 찾으며 가장 늦게 찾는 경우는 log₂10 = 3.32193(올림하면 4번)만에 찾습니다(log₂10의 진수가 10인 이유는 데이터 크기가 10이기 때문이며, 밑이 2인 이유는 연산을 할 때마다 2분의 1씩 연산 횟수가 줄어들기 때문).

이분탐색은 결국 n값에 따라 2분의 1씩 탐색 부분이 줄어들므로 최대 log₂n번의 비교를 한다면 찾고자 하는 수를 찾을 수 있습니다.

n값에 따라서 최악의 경우 logn번의 연산을 해야하는 경우는 빅오표기법으로 O(logn)으로 나타냅니다. 참고로 log₁₀n은 logn으로 표현할 수 있습니다. 이분탐색의 경우 log₂n번의 연산을 하지만 log₂n과 log₁₀n, 두 수식의 그래프의 모형은 비슷하므로 시간 복잡도로 표현할 때는 logn으로 표현해도 큰 문제가 되지 않습니다.

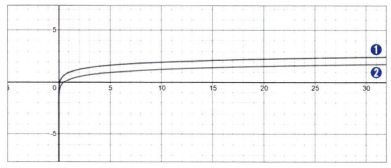
1은 logn 2는 log₂n 그래프

시간복잡도가 O(n²)인 경우

시간복잡도가 O(2ⁿ)인 경우

시간복잡도가 O(n!)인 경우