⚾Chapter05 외국인 투수 스카우팅 최적화 3 - 볼 배합 지표, 배럴 타구 허용 비율

2022-04-15 12 분 소요

성능 향상을 위한 방법📑

모델 구축과 검증 파트에서는 투수를 스카우트하는 모델을 구축함
스탯캐스트 데이터에 있는 투구 좌표와 구종 정보를 활용해 투수의 제구력을 평가하고 이닝별 상대한 타자 수를 통해 아웃 확률 을 산출해 최종적으로 2명의 투수를 스카우트함
스탯캐스트 데이터에는 그 외에도 투 구에 대한 다양한 정보가 기록돼 있음
성능 향상을 위한 방법에서는 스탯캐스트 데이터를 활용해 투수 평가 시 사용할 수 있는 추가 지표들을 탐색해볼 예정
투수의 볼 배합을 수치화할 수 있 는 방법을 탐구하고, 타구의 발사 각도와 속도를 활용한 지표도 활용함

1. 볼 배합 지표

투수는 각자 결정적인 순간에 던지는 본인만의 결정구를 지니고 있음
해당 결정구를 통 해 타자를 아웃시키기 위해서 결정구를 던지기 전까지 타자의 시선을 분산시키는 작업이 필 요함
타자의 시선을 흩트리고 리듬을 방해하기 위해서는 투구를 지그재그로 던지는 방법이 있음
가령 첫 번째 투구를 우측 상단에 던진 후 두 번째 투구를 좌측 하단에 던지면 타자는 상대적으로 공을 맞히기가 힘들 것을 보고, 이런 식으로 투구의 조합을 가져가는 것을 볼 배합이라고 함
좋은 볼 배합에 대한 기준은 명확히 정해진 것은 없으므로 볼 배합 능력을 수치화 하려면 먼저 좋은 볼 배합에 대한 기준을 정해야 함
여기서는 단순하게 순차적으로 던진 투구 간의 거리가 멀수록 좋은 볼 배합이라고 정의함

볼 배합의 정의를 내렸으니 스탯캐스트 데이터를 활용해 투수별 볼 배합의 정도를 수치화해 표현해봄

스탯캐스트 데이터를 불러오기

import pandas as pd
  
atKbo_11_18_StatCast = pd.read_csv("data/chap05/baseball_savant_foreigners_2011_2018.csv")
  
atKbo_11_18_StatCast.head(10)

	game_date	release_speed	batter	pitcher	events	description	zone	stand	p_throws	bb_type	…	plate_x	plate_z	ax	ay	az	launch_speed	launch_angle	release_spin_rate	pitch_name	pitcher_name
0	2010-10-09	93.0	425834.0	430962	field_out	hit_into_play	4.0	R	R	popup	…	-0.626	2.771	-6.404	26.077	-9.694	NaN	NaN	NaN	4-Seam Fastball	니퍼트
1	2010-10-09	95.2	150289.0	430962	home_run	hit_into_play_score	5.0	L	R	fly_ball	…	-0.112	2.401	-10.168	28.786	-8.895	NaN	NaN	NaN	4-Seam Fastball	니퍼트
2	2010-10-09	94.3	150289.0	430962	NaN	foul	2.0	L	R	NaN	…	0.272	3.052	-5.605	26.657	-7.794	NaN	NaN	NaN	4-Seam Fastball	니퍼트
3	2010-10-09	94.0	150289.0	430962	NaN	blocked_ball	13.0	L	R	NaN	…	-1.193	0.632	-9.099	30.273	-6.371	NaN	NaN	NaN	4-Seam Fastball	니퍼트
4	2010-10-09	92.8	150289.0	430962	NaN	ball	14.0	L	R	NaN	…	0.370	1.383	-5.846	27.290	-11.262	NaN	NaN	NaN	4-Seam Fastball	니퍼트
5	2010-10-09	80.8	150289.0	430962	NaN	foul_tip	13.0	L	R	NaN	…	-1.233	2.059	-10.897	18.539	-20.286	NaN	NaN	NaN	Changeup	니퍼트
6	2010-10-09	92.0	150289.0	430962	NaN	ball	9.0	L	R	NaN	…	0.510	1.722	-6.251	27.786	-10.031	NaN	NaN	NaN	4-Seam Fastball	니퍼트
7	2010-10-09	92.5	430632.0	430962	field_out	hit_into_play	13.0	L	R	line_drive	…	-1.010	2.212	-8.279	26.466	-8.376	NaN	NaN	NaN	4-Seam Fastball	니퍼트
8	2010-10-09	91.2	430632.0	430962	NaN	ball	13.0	L	R	NaN	…	-0.106	1.418	-9.239	25.490	-13.556	NaN	NaN	NaN	4-Seam Fastball	니퍼트
9	2010-10-09	91.8	430632.0	430962	NaN	ball	11.0	L	R	NaN	…	-1.426	2.971	-12.090	25.659	-15.250	NaN	NaN	NaN	2-Seam Fastball	니퍼트

10 rows × 24 columns

다음으로, 투수별 볼 배합 수치를 구하는 함수를 정의해 봄

알고리즘 구성

우선 특정 타자를 상대할 때 던진 첫 번째 투구와 두 번째 던진 투구의 거리를 구함
두 번째로 던진 투구와 세 번째 투구의 거리를 구함
마지막으로 n-1 번째로 던진 투구와 n 번째로 던진 투구의 거리를 구한 후, 모든 거리를 평균 내어 볼 배합 수치를 측정

투수별 볼 배합 수치를 구하는 함수를 정의

import numpy as np
  
def Compute_Distance(x1,y1,x2,y2):
    return ((x1 - x2)**2 + (y1 - y2)**2)**0.5
      
  
def Mean_Distance_Per_Batter(df):
    if df.shape[0] == 1 :
        return np.nan
      
    distances = []
    for i in range(df.shape[0]-1, 0, -1):
        distance = Compute_Distance(df['plate_x'].iloc[i], df['plate_z'].iloc[i],
                                    df['plate_x'].iloc[i-1], df['plate_z'].iloc[i-1])
        distances.append(distance)
          
    return np.mean(distances)

먼저 두 개의(X, y) 좌표 간의 거리를 구하는 함수 Compute_Distance를 정의
그러고 나서 Mean_Distance_Per_Batter 함수를 사용하면 해당 투수가 타자를 상대할 때 던진 투구 간의 평균 거리를 구할 수 있음
스탯캐스트 데이터는 데이터셋 기준으로 아래에서부터 위로 가는 방향으로 투구가 시간순으로 기록되어 있으므로, 아래에서부터 위로 순회하면서 순차적으로 투구 간의 거리를 구함
그 후 구한 거리의 평균을 구함

하나의 투구만 던지고 중도 교체됐을 때는 거리를 측정할 수 없으므로 NaN 값을 반환하게 함수를 설계

Mean_Distance_Per_Batter 함수를 적용

MDPB = atKbo_11_18_StatCast.groupby(
    ['pitcher_name', 'batter']).apply(Mean_Distance_Per_Batter)
MDPB
  
# 실행 결과
pitcher_name  batter  
니퍼트           110029.0    1.418679
              113028.0    1.262822
              116338.0    1.475932
              121347.0    1.922868
              123173.0    1.306911
                            ...   
휠러            543807.0    1.312943
              545350.0    3.023675
              594828.0         NaN
              608324.0    1.542978
              621043.0         NaN
Length: 11263, dtype: float64

스탯캐스트 데이터를 pitcher_name과 batter 기준으로 groupby 한 후 Mean_Distance_Per_ Batter 함수를 적용해 투수별로 상대한 타자에 대한 볼 배합 수치를 산출
해당 결과 에서 NaN 값은 제거한 후 투수 기준으로 groupby를 진행

그리고 투수별 평균 값 을 구해 각 투수에 대한 하나의 볼 배합 수치만 산출

투수별로 상대한 타자에 대한 볼 배합 수치를 산출

pitch_mix = MDPB.dropna().groupby('pitcher_name').mean()
pitch_mix.head()
  
# 실행 결과
pitcher_name
니퍼트      1.431813
다이아몬드    1.408325
듀브론트     1.469793
레나도      1.501783
레온       1.529366
dtype: float64

투구 간의 평균 거리를 산출해 투수별 볼 배합 지표를 산출
해당 지표와 선형회귀분석 파트에서 정의한 제구력 지표를 함께 활용해 다중선형회귀 모델을 구축하여 2019년도 외국인 투수를 스카우팅
지금까지 순차적으로 코드를 실행해 왔다면 Elite_11_18 변수에는 2011년도부터 2018년도까지 KBO에서 활약한 우수 외국인 투수들 의 KBO 첫 번째 시즌 성적과 더불어 MLB 스탯캐스트 데이터로 산출한 제구력 지표가 기록 돼 있음

Elite_11_18변수에 투수별 볼 배합 지표를 추가

  Elite_11_18['PMI'] = pitch_mix[Elite_11_18.pitcher_name].values
  Elite_11_18

	index	pitcher_name	year	team	ERA	TBF	H	HR	BB	HBP	SO	year_born	num_pitches	PMI
0	0	니퍼트	2011	두산	2.55	763	150	8	64	10	150	NaN	3	1.431813
1	8	다이아몬드	2017	SK	4.42	581	163	11	35	9	59	NaN	2	1.408325
2	12	레이예스	2013	SK	4.84	751	157	15	91	7	135	NaN	2	1.449854
3	14	레일리	2015	롯데	3.91	768	182	20	57	15	134	1988년 06월 29일	4	1.505396
4	25	린드블럼	2015	롯데	3.56	861	196	28	52	12	180	1987년 06월 15일	3	1.506041
5	37	보우덴	2016	두산	3.80	742	159	17	54	6	160	NaN	2	1.495359
6	43	샘슨	2018	한화	4.68	703	144	17	79	5	195	NaN	1	1.503132
7	45	세든	2013	SK	2.98	780	169	14	73	11	160	NaN	4	1.482919
8	48	소사	2012	KIA	3.54	614	137	9	39	8	104	NaN	3	1.526452
9	67	웨버	2014	NC	4.58	512	132	13	42	3	85	NaN	3	1.431382
10	103	윌슨	2018	LG	3.07	689	158	11	35	6	149	1989년 09월 25일	4	1.494486
11	75	탈보트	2012	삼성	3.97	584	136	8	54	5	68	NaN	2	1.438349
12	79	팻딘	2017	KIA	4.14	770	211	22	39	16	143	NaN	3	1.384081
13	82	피가로	2015	삼성	3.38	688	154	16	51	7	117	NaN	2	1.543786
14	84	피어밴드	2015	넥센	4.67	774	202	23	61	12	137	NaN	2	1.325846
15	88	해커	2013	NC	3.63	744	163	12	50	17	127	NaN	3	1.409816
16	97	헥터	2016	KIA	3.40	868	211	7	51	6	139	NaN	3	1.386480
17	100	후랭코프	2018	두산	3.74	621	118	12	55	22	134	1988년 08월 27일	1	1.767966

Elite_11_18에 기록된 투수들만 pitch_mix 변수에서 추출한 후 해당 투수들의 볼 배합 지수를 Elite_11_18의 PMI 칼럼에 기록

다음으로 statsmodels 패키지를 사용해 다중선형회귀 분석을 실시하고 결과 리포트를 확인

다중선형회귀 분석

import statsmodels.api as sm
  
y = Elite_11_18.ERA.values
X = sm.add_constant(Elite_11_18[['num_pitches', 'PMI']].values)
  
model = sm.OLS(y, X)
  
result = model.fit()
  
result.summary()

OLS Regression Results

Dep. Variable:	y	R-squared:	0.417
Model:	OLS	Adj. R-squared:	0.339
Method:	Least Squares	F-statistic:	5.365
Date:	Fri, 15 Apr 2022	Prob (F-statistic):	0.0175
Time:	08:17:15	Log-Likelihood:	-12.201
No. Observations:	18	AIC:	30.40
Df Residuals:	15	BIC:	33.07
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
const	9.0464	2.216	4.082	0.001	4.322	13.770
x1	-0.4438	0.144	-3.077	0.008	-0.751	-0.136
x2	-2.7600	1.410	-1.957	0.069	-5.766	0.246

Omnibus:	2.157	Durbin-Watson:	1.577
Prob(Omnibus):	0.340	Jarque-Bera (JB):	0.664
Skew:	-0.351	Prob(JB):	0.717
Kurtosis:	3.627	Cond. No.	69.1

MLB에서의 제구력 지표와 볼 배합 지수를 활용해 KBO 첫 번째 시즌의 ERA를 예측하는 다중선형회귀 모델을 구축함
const는 상수항, xl은 제구력 지표, x2는 볼 배합 지수인 PMI를 뜻함
제구력 지표가 1 증가할 때마다 KBO 첫 번째 시즌의 ERA가 평균적으로 0.44 감소하는 것을 알 수 있고, 불 배합 지표는 1 증가할 때마다 ERA가 평균적으로 2.76 감소하는 것을 알 수 있음
하지만 모든 계수가 0.05 수준에서 통계적으로 유의하지는 않음
x2의 계수의 p-value가 0.069인 것으로 나왔지만, 이는 모델 구축에 사용된 데이터의 개수가 적어서 발생할 수도 있으므로 추후 데이터가 더 확보되면 다시 검증해볼 필요가 있음
이번 절에서는 예측하는 단계까지의 전체 과정 실습을 위해 해당 모델을 계속 활용함

2019년도 투수들의 KBO 첫 번째 시즌 ERA 예측을 위해선 투수들의 제구력 지표와 볼 배합 지표가 필요

2019년도 투수의 볼 배합 지표를 산줄

MDPB_19 = atKbo_19_StatCast.groupby(['pitcher_name', 'batter']). \
    apply(Mean_Distance_Per_Batter)
pitch_mix_19 = MDPB_19.dropna().groupby('pitcher_name').mean()
pitch_mix_19.head()
  
# 실행 결과
pitcher_name
루친스키    1.508374
맥과이어    1.412896
버틀러     1.469185
서폴드     1.510175
알칸타라    1.382733
dtype: float64

pitch_mix_19 변수에 2019년 외국인 투수들의 볼 배합 지수가 저장

아웃확률 추정하기에서 투수의 2019년 제구력 지표를 기록한 coordEdge_19에 투수들의 볼 배합 지수를 나타내는 PMI 칼럼을 추가함

볼 배합 지수를 coordEdge_19의 PMI 칼럼에 추가

coordEdge_19['PMI'] = pitch_mix_19[coordEdge_19.pitcher_name].values
coordEdge_19

	pitcher_name	num_pitches	PMI
0	루친스키	4	1.508374
1	맥과이어	3	1.412896
2	버틀러	2	1.469185
3	서폴드	3	1.510175
4	알칸타라	3	1.382733
5	요키시	3	1.476024
6	윌랜드	2	1.497783
7	채드벨	4	1.446687
8	켈리	3	1.483089
9	쿠에바스	4	1.503062
10	터너	3	1.443403
11	톰슨	3	1.609576
12	헤일리	3	1.576976

투수의 2019년도 제구력 지표는 num_pitches에, 볼 배합 지표는 PMI에 기록돼 있음

해당 값을 predict 함수에 입력해 2019년도 투수들의 KBO 첫 번째 시즌 ERA 예측값을 얻을 수 있음

2019년도 투수들의 KBO 첫 번째 시즌 ERA 예측값

test_X = sm.add_constant(coordEdge_19[['num_pitches', 'PMI']].values)
coordEdge_19['pred'] = result.predict(test_X)
coordEdge_19.sort_values('pred')

	pitcher_name	num_pitches	PMI	pred
0	루친스키	4	1.508374	3.108067
9	쿠에바스	4	1.503062	3.122727
11	톰슨	3	1.609576	3.272562
7	채드벨	4	1.446687	3.278323
12	헤일리	3	1.576976	3.362537
3	서폴드	3	1.510175	3.546906
8	켈리	3	1.483089	3.621663
5	요키시	3	1.476024	3.641163
10	터너	3	1.443403	3.731196
1	맥과이어	3	1.412896	3.815397
4	알칸타라	3	1.382733	3.898646
6	윌랜드	2	1.497783	4.024921
2	버틀러	2	1.469185	4.103848

statsmodels.api에서 제공하는 다중선형회귀 모델을 활용하여 예측값을 산출할 때는 x1, x2 변수뿐만 아니라 상수항까지 입력해야 함
add_constant 함수를 활용해 상수항을 추가한 후 predict 함수를 활용해 예측값을 산출
예측값을 coordEdge_19의 pred 칼럼에 저장한 후 오름차순으로 정렬해 값을 비교
루친스키와 쿠에바스의 ERA 가 가장 낮게 산출됐으므로 루친스키와 쿠에바스를 스카우팅 함.
이처럼 스탯캐스트의 데이터를 가공하여 만든 볼 배합 지수를 제구력 지표와 함께 활용해 MLB 투수들의 KBO에서 ERA 성적을 추정할 수 있으며, 해당 추정치를 투수 스카우팅에 활용할 수 있음

2. 배럴 타구 허용 비율

측정 장비의 발달 덕분에 2015년부터는 공의 발사각도와 속도까지 측정할 수 있게 됨
새로운 요소가 측정됨에 따라 다양한 파생 지표를 산출 가능
그중 배럴 타구는 2015년도부터 타구 속도와 발사각도의 조합상 평균적으로 타율 .500. 장타율 1.500 이상을 생산하는 타구로 정의함
해당 타구는 타자 입장에서 좋은 성적이 나오므로 타자들이 목표로 하는 타구라고 볼 수 있음
반면, 투수는 타자와 반대되는 입장에 있 어 배럴 타구가 나오는 것을 최소화해야 함
투수가 배럴 타구를 허용한 개수를 전체 투구 개수로 나누면 배럴 타구 허용 비율이 산출
해당 지표가 가장 작은 2명의 2019년 도 투수를 스카우팅해 봄
MLB 공식 홈페이지에 게시된 배럴 타구의 정의에 따르면 배럴 타구가 되기 위해서는 타구 속도가 최소 98mph여야 하며, 이때 발사각도는 26〜30도 사이여야 함
1mph가 증가 할 때마다 허용되는 발사각도의 범위는 넓어지며, 116mph 이상부터는 발사각도 8~50도 사이에 있으면 모두 배럴 타구로 분류함
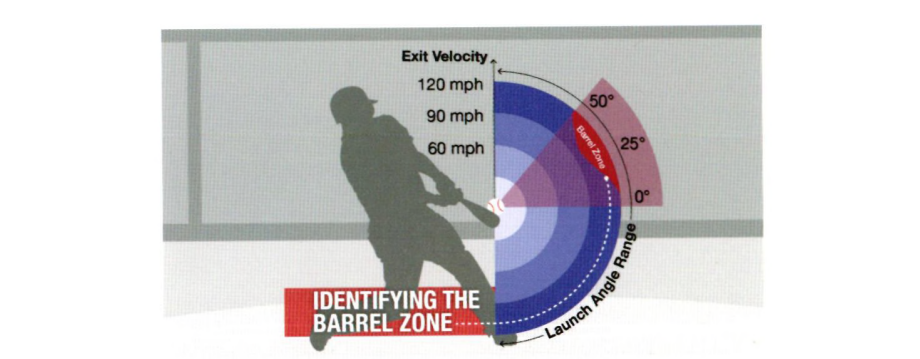
위의 그림은 배럴 타구를 시각화한 그림
빨간색의 Barrel Zone에 속하는 타구가 배럴 타구가 됨
배럴 타구를 정의했으니 배럴 타구 허용 비율을 산출하는 함수를 구축해봄
스탯캐스트 데이터를 정제하여 투수별 허용한 배럴 타구와 던진 전체 투구 개수를 구한 후 배럴 타구 수를 전체 투구 수로 나누는 함수를 구축

배럴 타구 수를 구하는 countBarrelPitches 함수를 정의

배럴 타구 수를 구하는 함수를 정의

def countBarrelPitches(df):    
    lower = 26
    upper = 30
  
    QL = []
  
    for mph in range(98, int(df.launch_speed.max())+1):
        if mph <= 115:
            QL.append(df.query(f'(launch_speed >= {mph} & launch_speed < {mph+1}) & \
                                 (launch_angle >= {lower} & launch_angle <= {upper})'))
            lower -= 1
            upper += 20/18
  
        else:
            QL.append(df.query(f'(launch_speed >= {mph} & launch_speed < {mph+1}) & \
                                 (launch_angle >= {lower} & launch_angle <= {upper})'))
  
    BarrelPitches = (pd.concat(QL, axis = 0).
                     groupby('pitcher_name')['game_date'].
                     count().
                     reset_index())
    BarrelPitches = BarrelPitches.rename({'game_date':'barrel_pitches'}, axis = 1)
      
    return BarrelPitches

먼저 발사각도의 하한선과 상한선을 각각 26도와 30도로 정해줌
그후 타구의 속도가 98mph 이상 99mph 미만일 때 주어진 발사각도에 해당하는 투구를 스탯캐스트 데이터셋으로부터 추출하고 리스트에 저장해둠
타구의 속도가 1 증가할 때마다 발사각도 하한선은 1 씩 감소하면서 범위를 넓혀주고 상한선은 20/18씩 증가하면서 범위를 넓혀줌
최종적으로 타구의 속도가 116일 때 하한선이 8도가 되고 상한선이 50도가 될 것임
이 과정을 스탯캐스트 데이터에 기록된 가장 빠른 타구 속도에 다다를 때까지 반복함
반복문이 완료되면 QL 리스트에 저장된 데이터셋을 concat 함수를 사용해 결합한 후 pitcher_name을 기준으로 묶어주고 행의 개수를 산출하면 투수별 배럴 타구 수를 확인 가능

해당 함수를 atKbo_19_StatCast에 적용한다면 다음과 같은 결과를 얻게 됨

함수를 atKbo_19_StatCast에 적용

countBarrelPitches(atKbo_19_StatCast).head()

	pitcher_name	barrel_pitches
0	루친스키	9
1	맥과이어	16
2	버틀러	57
3	서폴드	26
4	알칸타라	18

다음으로는 타자가 던진 총투구 수를 구하는 함수를 정의하고, 함수 결과를 확인해봄

타자가 던진 총투구 수를 구하는 함수를 정의

def countTotalPitches(df):
    TotalPitches = df.groupby('pitcher_name')['game_date'].count().reset_index()
    TotalPitches = TotalPitches.rename({'game_date':'total_pitches'}, axis = 1)
      
    return TotalPitches
  
countTotalPitches(atKbo_19_StatCast).head()

	pitcher_name	total_pitches
0	루친스키	930
1	맥과이어	925
2	버틀러	4454
3	서폴드	1860
4	알칸타라	824

스탯캐스트 데이터를 pitcher_name 기준으로 묶어준 후 행의 개수를 산출하면 해당 투수가 던진 총 투구 수를 구할 수 있음

마지막으로 배럴 타구 수를 총 투구 수로 나누는 함수를 정의

배럴 타구 수를 총투구 수로 나누는 함수를 정의

def getBarrelRatio(df): 
    BarrelPitches_result = countBarrelPitches(df)
    TotalPitches_result = countTotalPitches(df)
      
    pitches = pd.merge(BarrelPitches_result, TotalPitches_result, on='pitcher_name',
                       how='right')
    pitches = pitches.fillna(0)
    pitches['barrel_ratio'] = pitches['barrel_pitches'] / pitches['total_pitches']
    return pitches.sort_values('barrel_ratio')

스탯캐스트 데이터에 countBarrelPitches 함수와 countTotalPitches 함수를 적용한 결과물을 각각 BarrelPitches_result, TotalPitches_result에 저장
merge 함수를 사용해 BarrelPitches_result 데이터프레임과 TotalPitches_result 데이터프레임을 합칠 때 TotalPitches_result를 기준으로 병합을 실시
BarrelPitches_result에 있는 투수들은 모두 TotalPitches_result 데이터프레임에도 존재할 것이므로 barrel_pitches 값 과 total_pitches 값이 함께 표시됨
배럴 타구를 하나도 허용하지 않은 투수는 BairrelPitches_result에 값이 없으므로 merge 사용 시 NaN 값이 기록
fillna 함수 를 사용해 모든 NaN을 0으로 대체하고 barrel_pitches 값을 total_pitches 값으로 나누면 투수별 배럴 타구 허용 비율이 산출
배럴 타구는 적게 허용할수록 좋으므로 barrel_ratio 지표는 0에 가까울수록 좋은 지표가 됨
그러므로 barrel_ratio 기준으로 오름차 순 정렬하여 값을 반환함
getBarrelRatio 함수를 atKbo_19_StatCast 변수에 적용하여 2019년 외국인 투수들의 배럴 타구 허용 비율을 산출할 수 있음
하지만 launch_speed와 launch_angle에는 결측값이 다량 존재함

결측값이 기록된 투구는 배럴 타구 여부를 판단할 수 없으므로 launch_speed와 launch_angle에 결측값이 존재하는 투구는 제거한 후 getBarrelRatio 함수를 적용함

결측값 제거 후 함수를 적용

Stat19notnull = atKbo_19_StatCast[atKbo_19_StatCast.launch_speed.notnull() & \
                                  atKbo_19_StatCast.launch_angle.notnull()]
getBarrelRatio(Stat19notnull)

	pitcher_name	barrel_pitches	total_pitches	barrel_ratio
11	헤일리	6	154	0.038961
0	루친스키	9	226	0.039823
2	버틀러	57	1215	0.046914
3	서폴드	26	554	0.046931
10	톰슨	28	561	0.049911
7	켈리	14	280	0.050000
1	맥과이어	16	263	0.060837
6	채드벨	24	377	0.063660
8	쿠에바스	8	120	0.066667
9	터너	26	372	0.069892
4	알칸타라	18	253	0.071146
5	윌랜드	5	67	0.074627

notnull 함수와 & 연산자를 활용하여 launch_speed와 launch_angle이 모두 기록된 행만 추 출해 Stat19notnull 변수에 저장
그 후 getBarrelRatio를 활용하여 투수들의 배럴 타구 허용 비율을 산출
헤일리와 루친스키의 배럴 타구 허용 비율이 가장 낮으므로 해 당 투수들을 스카우팅하는 결정을 내릴 수 있지만 launch_speed와 launch_angle 이 기록된 투구만 추출하는 과정에서 많은 데이터 손실이 발생했으므로 충분한 데이터를 활 용하여 투수들을 평가하지 못했다는 한계점이 존재함
결측된 데이터를 확보할 수 있다면 투수를 더욱 정교하게 평가하여 향상된 의사결정이 가능할 것으로 기대

정리📑

지금까지 외국인 투수 스카우팅 최적화 경진대회에 참가한 내용을 소개함
탐색적 데이터 분석에서 시작해, 유의미한 통곗값을 얻기 위한 데이터 전처리, 제구력이 좋을수록 ERA가 낮아진다는 가설 검증을 통한 모델링, 그리고 투수 평가 시 추가로 활용할 수 있는 지표들 을 탐구
또한 파이썬 언어와 판다스, 넘파이 등의 패키지를 활용해 데이터를 분석하는 예제를 실습
데이터 분석은 질문을 떠올리고 해당 질문의 답을 찾아가는 과정의 반복
여기서는 야구 데이터로 실습했지만, 전반적인 사고의 흐름은 분야에 관계없이 비슷할 것임
본인이 관심 있는 분야의 데이터를 활용해 궁금한 내용에 대한 답을 찾기 위해 분석한다면 분석 역량이 빠르게 쌓이는 것을 경험할 수 있을 것으로 기대함

Twitter Facebook LinkedIn

⚾Chapter05 외국인 투수 스카우팅 최적화 3 - 볼 배합 지표, 배럴 타구 허용 비율

성능 향상을 위한 방법📑

1. 볼 배합 지표

2. 배럴 타구 허용 비율

정리📑

공유하기

댓글남기기

참고

시간복잡도(time complexity)는 어떻게 계산하는가?

소프트웨어 디자인 패턴(Design Pattern)은 무엇인가?

⚾Chapter05 외국인 투수 스카우팅 최적화 2 - 데이터 전처리, 모델 구축과 검증

⚾Chapter05 외국인 투수 스카우팅 최적화 1 - 문제 정의, 탐색적 데이터 분석