⚾Chapter05 외국인 투수 스카우팅 최적화 2 - 데이터 전처리, 모델 구축과 검증

2022-04-15 30 분 소요

데이터 전처리📑

예측 모델을 구축하는 데 사용하는 데이터 유형은 다음과 같이 나눌 수 있음.
- 학습(train) 데이터 : 모델을 학습할 때 사용
- 검증(validation) 데이터 :학습된 모델을 튜닝할 때 사용
- 테스트(test) 데이터 : 모델의 성능을 시험
성능 좋은 모델을 구축하기 위해서는 튜닝도 중요하지만, 양질의 데이터로 구성된 학습 데이터가 필요
Garbage in Garbage out 현상 : 모델은 학습 데이터를 바탕으로 구축되는데, 학습 데이터의 질이 나쁘면 모델의 성능 또한 좋지 않은 현상

1. 가설을 확인하기 위한 투수 집단 선정하기

데이터 분석에서는 논리를 바탕으로 데이터 분석을 진행해 최종 결과물을 도출해야 함
- 가설을 세우고, 가설에 문제가 없음을 밝힘으로써 데이터 분석을 전개
- 가설의 참 • 거 짓을 확인하기 위해서는 가설을 어떻게 정량적으로 측정할 것인지 결정
이번 대회에서 세운 가설은 “KBO에서 우수한 활약을 보인 투수들은 MLB에서 제구 력이 뛰어날 것이다.”
이 가설의 참 • 거짓 판별을 위해서는 다음을 결정해야 함
1. 가설 확인의 대상이 되는 투수는 누구인가? (3_1)
2. KBO에서의 우수한 활약은 어떻게 측정할 것인가? (3_2)
3. MLB에서의 제구력은 어떻게 측정할 것인가? (4)
이 가설은 MLB에서의 투구 기록과 KBO에서의 투구 기록이 모두 기록된 투수에 대해서만 확인 가능

해당 조건에 부합하는 선수를 추출하기 위해 데이터를 살펴봄

대화에서 제공한 데이터를 불러오기

import pandas as pd
  
#데이터셋 불러오기 
atKbo_11_18_KboRegSsn = pd.read_csv("data/chap05/kbo_yearly_foreigners_2011_2018.csv")
  
atKbo_11_18_MlbTot = pd.read_csv("data/chap05/fangraphs_foreigners_2011_2018.csv")
  
atKbo_11_18_StatCast = pd.read_csv("data/chap05/baseball_savant_foreigners_2011_2018.csv")
  
atKbo_19_MlbTot = pd.read_csv("data/chap05/fangraphs_foreigners_2019.csv")
  
atKbo_19_StatCast = pd.read_csv("data/chap05/baseball_savant_foreigners_2019.csv")

pandas 패키지의 read_csv() 함수를 활용해 CSV 파일을 읽을 수 있음

변수별 저장된 데이터 개요

2011 년부터 2018년까지 KBO에서 활약한 외국인 투수

변수명	내용
atKbo_11_18_KboRegSsn	역대 KBO 정규시즌 성적
atKbo_11_18_MlbTot KBO	입성 전 MLB에서의 역대 정규시즌 성적
atKboJ1 _18_StatCast KBO	입성 전 MLB에서의 스탯캐스트 데이터

2019년 신규 KBO 외국인 투수

변수명	내용
atKbo_19_MlbTot	MLB에서의 역대 정규시즌 성적
atKboJ9_StatCast	MLB에서의 스탯캐스트 데이터

데이터별 상위 10개 행을 확인

pd.DataFrame.head() 힘수를 통해 확인 가능

KBO 정규시즌 성적

atKbo_11_18_KboRegSsn.head(10)

	pitcher_name	year	team	ERA	TBF	H	HR	BB	HBP	SO	year_born
0	니퍼트	2011	두산	2.55	763	150	8	64	10	150	NaN
1	니퍼트	2012	두산	3.20	785	156	15	68	8	126	NaN
2	니퍼트	2013	두산	3.58	482	108	7	34	4	104	NaN
3	니퍼트	2014	두산	3.81	760	186	17	48	6	158	NaN
4	니퍼트	2015	두산	5.10	404	104	4	33	4	76	NaN
5	니퍼트	2016	두산	2.95	701	151	15	57	9	142	NaN
6	니퍼트	2017	두산	4.06	782	175	20	77	10	161	NaN
7	니퍼트	2018	KT	4.25	765	209	26	39	9	165	NaN
8	다이아몬드	2017	SK	4.42	581	163	11	35	9	59	NaN
9	듀브론트	2018	롯데	4.92	629	162	13	62	8	109	NaN

KBO 기록에는 팀 소속과 더불어 연도별 ERA, TBF, H, HR 등의 지표가 기록

MLB 정규시즌 성적

atKbo_11_18_MlbTot.head(10)

	pitcher_name	year	ERA	WAR	TBF	H	HR	BB	HBP	SO	WHIP	BABIP	FIP	LD%	GB%	FB%	IFFB%	SwStr%	Swing%
0	오간도	2011.0	3.51	3.3	693.0	149.0	16.0	43.0	7.0	126.0	1.14	0.265	3.65	0.237	0.364	0.674	0.147	0.090	0.475
1	험버	2011.0	3.75	3.2	676.0	151.0	14.0	41.0	6.0	116.0	1.18	0.275	3.58	0.168	0.471	0.458	0.094	0.092	0.463
2	루카스	2012.0	3.76	2.8	827.0	185.0	13.0	78.0	1.0	140.0	1.36	0.289	3.75	0.203	0.572	0.707	0.082	0.062	0.424
3	다이아몬드	2012.0	3.54	2.2	714.0	184.0	17.0	31.0	4.0	90.0	1.24	0.292	3.94	0.210	0.534	0.597	0.040	0.068	0.467
4	듀브론트	2013.0	4.32	2.2	705.0	161.0	13.0	71.0	5.0	139.0	1.43	0.310	3.78	0.199	0.456	0.633	0.127	0.077	0.434
5	스와잭	2017.0	2.33	2.2	303.0	58.0	6.0	22.0	2.0	91.0	1.03	0.286	2.74	0.155	0.439	0.485	0.145	0.142	0.500
6	듀브론트	2012.0	4.86	1.3	709.0	162.0	24.0	71.0	5.0	167.0	1.45	0.312	4.37	0.234	0.437	0.635	0.086	0.096	0.442
7	탈보트	2010.0	4.41	1.2	696.0	169.0	13.0	69.0	8.0	88.0	1.49	0.301	4.48	0.169	0.478	0.495	0.070	0.060	0.428
8	비야누에바	2011.0	4.04	1.2	454.0	103.0	11.0	32.0	4.0	68.0	1.26	0.271	4.10	0.219	0.356	0.462	0.151	0.078	0.433
9	비야누에바	2014.0	4.64	1.2	343.0	89.0	6.0	19.0	3.0	72.0	1.39	0.342	3.13	0.202	0.413	0.474	0.161	0.113	0.486

MLB 기록에는 연도별 ERA, TBF, H, HR 등의 지표와 더불어 LD%, GB%, FB%, IFFB% 등 의 지표가 기록

스탯캐스트 데이터

atKbo_11_18_StatCast.head(10)

	game_date	release_speed	batter	pitcher	events	description	zone	stand	p_throws	bb_type	…	plate_x	plate_z	ax	ay	az	launch_speed	launch_angle	release_spin_rate	pitch_name	pitcher_name
0	2010-10-09	93.0	425834.0	430962	field_out	hit_into_play	4.0	R	R	popup	…	-0.626	2.771	-6.404	26.077	-9.694	NaN	NaN	NaN	4-Seam Fastball	니퍼트
1	2010-10-09	95.2	150289.0	430962	home_run	hit_into_play_score	5.0	L	R	fly_ball	…	-0.112	2.401	-10.168	28.786	-8.895	NaN	NaN	NaN	4-Seam Fastball	니퍼트
2	2010-10-09	94.3	150289.0	430962	NaN	foul	2.0	L	R	NaN	…	0.272	3.052	-5.605	26.657	-7.794	NaN	NaN	NaN	4-Seam Fastball	니퍼트
3	2010-10-09	94.0	150289.0	430962	NaN	blocked_ball	13.0	L	R	NaN	…	-1.193	0.632	-9.099	30.273	-6.371	NaN	NaN	NaN	4-Seam Fastball	니퍼트
4	2010-10-09	92.8	150289.0	430962	NaN	ball	14.0	L	R	NaN	…	0.370	1.383	-5.846	27.290	-11.262	NaN	NaN	NaN	4-Seam Fastball	니퍼트
5	2010-10-09	80.8	150289.0	430962	NaN	foul_tip	13.0	L	R	NaN	…	-1.233	2.059	-10.897	18.539	-20.286	NaN	NaN	NaN	Changeup	니퍼트
6	2010-10-09	92.0	150289.0	430962	NaN	ball	9.0	L	R	NaN	…	0.510	1.722	-6.251	27.786	-10.031	NaN	NaN	NaN	4-Seam Fastball	니퍼트
7	2010-10-09	92.5	430632.0	430962	field_out	hit_into_play	13.0	L	R	line_drive	…	-1.010	2.212	-8.279	26.466	-8.376	NaN	NaN	NaN	4-Seam Fastball	니퍼트
8	2010-10-09	91.2	430632.0	430962	NaN	ball	13.0	L	R	NaN	…	-0.106	1.418	-9.239	25.490	-13.556	NaN	NaN	NaN	4-Seam Fastball	니퍼트
9	2010-10-09	91.8	430632.0	430962	NaN	ball	11.0	L	R	NaN	…	-1.426	2.971	-12.090	25.659	-15.250	NaN	NaN	NaN	2-Seam Fastball	니퍼트

10 rows × 24 columns

스탯캐스트 데이터에는 투구별 속성값이 기록된 것을 확인할 수 있습니다. 구속, 투구 결과, 구종 이름등이 기록
데이터별로 기록된 칼럼이 다르지만 투수의 이름 정보는 모든 데이터에서 pitcher.name 칼럼에 기록
그런데 2011년부터 2018년 사이에 기록된 데이터라서 중복된 이름 존재

데이터별로 고유 투수 이름을 확인하기 위해 판다스에 서 제공되는 pd.Series.unique() 함수를 사용

고유 투수 이름 확인

print('KBO:', len(atKbo_11_18_KboRegSsn['pitcher_name'].unique()))
print('MLB:', len(atKbo_11_18_MlbTot['pitcher_name'].unique()))
print('StatCast:', len(atKbo_11_18_StatCast['pitcher_name'].unique()))
  
# 실행 결과
KBO: 62
MLB: 60
StatCast: 60

KBO, MLB, 스탯캐스트 데이터에는 각각 62, 60, 60명의 고유 투수가 존재
데이터 집단별로 기록된 투수의 수가 다름

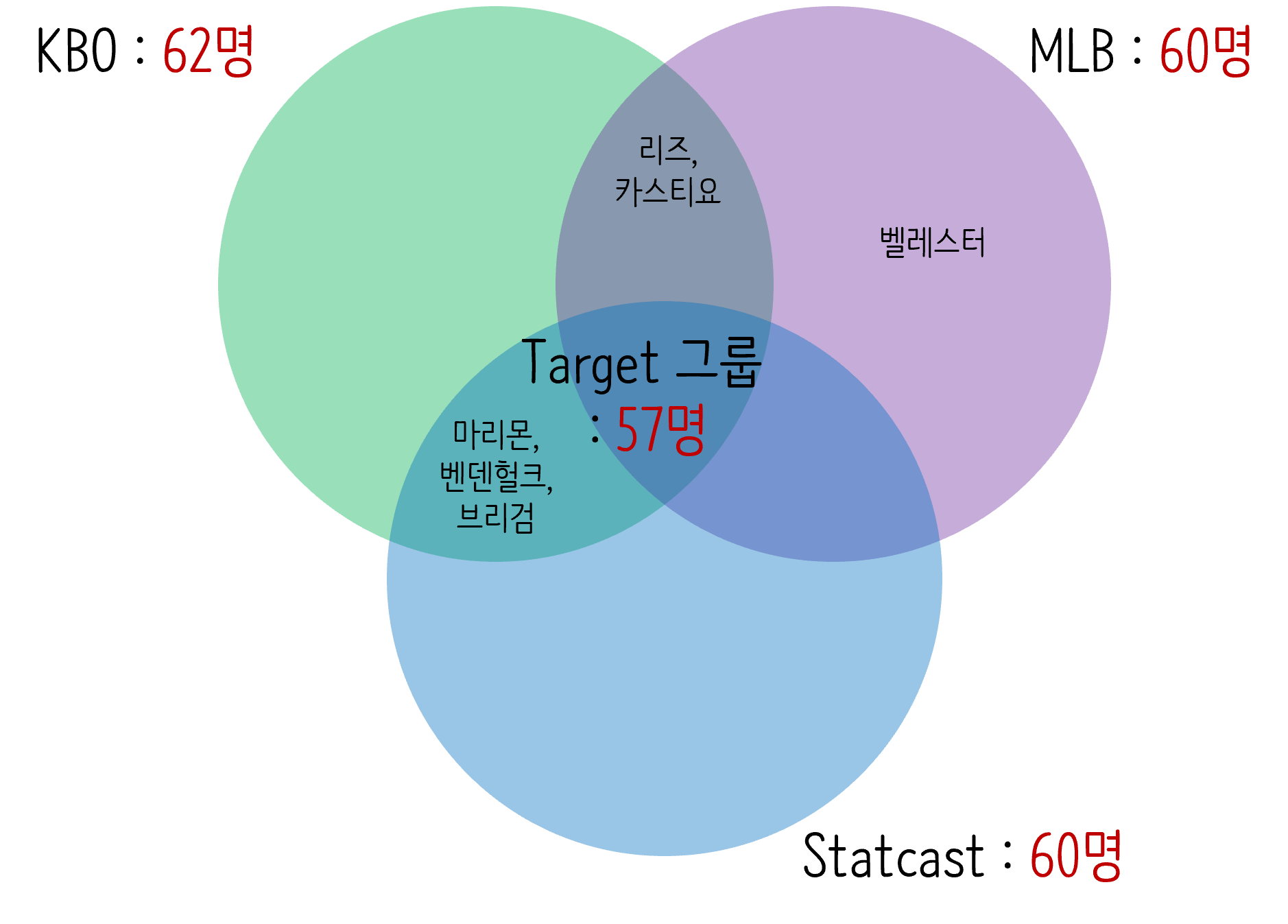
데이터 집단별 선수 분포
앞에서 세운 가설을 확인하려면 MLB와 KBO에 모두 기록된 선수가 필요
KBO, MLB. 스탯캐스트에는 각각 다른 투수가 기록
- 예를 들어 벨레스터 선수는 MLB 데이터에만 기록이 존재하고, 리즈와 카스티요 선수는 KBO와 MLB 데이터에는 기록이 있지만 스탯캐스트 데이터에는 기록이 없음
- 가설을 확인하기 위해 3개의 데이터 집단 모 두에서 기록이 존재하는 선수를 추출
- 위 그림에서 중앙에 있는 57명은 KBO, MLB, 스탯캐스트 데이터에 모두 기록된 투수이며 해당 투수 집단을 타깃(target) 집단이라고 정함

투수 이름은 pitcher_name 칼럼 에 기록돼 있으며, 데이터별 pitcher_name의 교집합을 구하기 위해 파이썬의 집합 연산을 사용

타깃 집단에 속한 투수를 추출

target = (set(atKbo_11_18_KboRegSsn['pitcher_name']) & 
          set(atKbo_11_18_MlbTot['pitcher_name']) &
          set(atKbo_11_18_StatCast['pitcher_name']))
  
print(type(target)) 
  
target = sorted(list(target))
  
print(type(target)) 
  
print(len(target))
  
# 실행 결과
<class 'set'>
<class 'list'>
57

파이썬에서는 set 타입에 대해 집합 연산을 지원하며, set() 함수를 통해 다른 데이터 타입을 set으로 변환 가능
위의 코드에서는 Series 형태인 데이터를 set 형태로 변환한 뒤, & 연산자를 통해 교집합을 추출
추출된 타깃 집단에는 57명의 투수가 존재
이렇게 KBO, MLB, 스탯캐스트 데이터에 기록이 존재하는 타깃 집단이 추출됨

외국인 투수 스카우팅은 선수 육성 차원보다는 팀 성적 향상에 즉시 기여할 수 있는 선수를 찾는 것이 목적이기 때문에 해당 투수의 KBO에서의 투수 능력 측정은 KBO 첫 번째 시즌의 평균자책점을 통해 평가

투수별로 KBO 첫 번째 시즌의 데이터를 추출

_idx = atKbo_11_18_KboRegSsn.query('pitcher_name in @target'). \
    groupby('pitcher_name')['year'].idxmin().values
firstYearInKBO_11_18 = atKbo_11_18_KboRegSsn.loc[_idx,:]
firstYearInKBO_11_18.head()

	pitcher_name	year	team	ERA	TBF	H	HR	BB	HBP	SO	year_born
0	니퍼트	2011	두산	2.55	763	150	8	64	10	150	NaN
8	다이아몬드	2017	SK	4.42	581	163	11	35	9	59	NaN
9	듀브론트	2018	롯데	4.92	629	162	13	62	8	109	NaN
10	레나도	2017	삼성	6.80	243	70	11	27	6	28	NaN
11	레온	2016	삼성	11.25	40	16	2	1	1	7	NaN

KBO 데이터에서 타깃 집단에 있는 투수들을 pd.DataFrame.query()함수를 통해 추출
query() 함수 안에는 함수 특성상 문자열이 입력돼야 함
문자열로는 환경에 저장된 변수 접근이 불가능하지만, 문자열 내에 특수문자 @을 사용하면 현재 환경에 있는 target 변수에 접근 가능
그후 groupby 함수를 통해 pitcher_name별로 데이터를 묶고 나서 year 값이 가장 작은 인덱스를 추출해 _idx 변수에 저장
가장 작은 year 값이 해당 투수의 KBO 첫 번째 시즌
추출된 인덱스를 활용해 KBO 데이터를 인덱싱하면 타깃 집단의 KBO 첫 번째 시즌 성적이 추출

2. 유효한 데이터 선정하기

총 57명 투수의 KBO에서의 첫 번째 시즌 성적을 추출했지만 모든 투수의 기록이 유효하지는 않음
예시
- 갑과 을 중에서 가위바위보를 누가 더 잘하는지를 평가하기 위 해서는 각각의 가위바위보 승률을 확인
- 갑은 승률이 100%이고 을은 승률이 40%라면 갑이 가위바위보를 더 잘한다고 평가 가능
- 하지만 갑은 가위바위보를 한 번 시도했고, 을은 100번 시도했다면 갑의 승률은 신뢰성 있는 지표라고 할 수 없을 것
야구에서도 투수의 활약상을 평가할 때 대표적으로 쓰이는 지표는 평균자책점이고 이 지표는 낮을수록 좋은 지표
가위바위보에서 승률이 가위바위보를 시도해야 기록되는 것처럼 평균자책점 또한 투수가 타자를 상대해야 기록되는 지표

그렇기에 평균자책점은 투수가 상대한 타자의 수(Total Batters Faced, TBF)에 영향을 받는 지표

투수 A	투수 B
ERA : 2.45	ERA : 2.00
TBF : 100	TBF : 20

ERA와 TBF 간의 관계

위의 표와 같이 투수 A와 투수 B가 있다고 가정
- 투수 A는 ERA가 2.45고 투수 B는 2.00일 때 투수 B가 더 잘한다고 평가 가능
- 하지만 투수가 상대한 타자 수를 확인해 보니 투수 A는 100명의 타자를 투수 B는 20명의 타자를 상대했다는 것을 알수 있음
- 시행 횟수가 충분하지 않기 때문에 이런 경우 투수 B의 ERA 2.00은 투수 B를 정확하게 평가하는 지표라고 보기에는 한계가 있음
반면, 투수 A는 100명의 타자를 상대했을 때 기록된 ERA가 2.45이므로 비교적 신뢰도가 높고 질이 좋은 데이터라고 볼 수 있음
여기서는 ‘Garbage In Garbage Out’ 이론에 기반해 상대한 타자 수가 특정 횟수 이상인 기록 추출
TBF 특성상 분산이 커서 평균으로 할 경우 이상치에 영향을 받기 때문에 특정 횟수는 타깃 집단 투수의 TBF의 중앙값으로 정의
ERA가 전체의 중앙값 이하인 투수를 우수한 활약을 보인 투수라고 정의할 것이기 때문에 TBF뿐만 아니라 ERA도 타깃 집단 투수의 ERA의 중앙값보다 작은 기록만 추출

ERA 또한 분산이 커서 평균 대신 중앙값을 기준함

TBF가 중앙값 이상이고 ERA가 중앙값 이하인 투수를 추출

TBF_median = firstYearInKBO_11_18['TBF'].median()
ERA_median = firstYearInKBO_11_18['ERA'].median()
Elite_11_18 = firstYearInKBO_11_18.query('TBF >= @TBF_median & ERA <= @ERA_median')
Elite_11_18

	pitcher_name	year	team	ERA	TBF	H	HR	BB	HBP	SO	year_born
0	니퍼트	2011	두산	2.55	763	150	8	64	10	150	NaN
8	다이아몬드	2017	SK	4.42	581	163	11	35	9	59	NaN
12	레이예스	2013	SK	4.84	751	157	15	91	7	135	NaN
14	레일리	2015	롯데	3.91	768	182	20	57	15	134	1988년 06월 29일
25	린드블럼	2015	롯데	3.56	861	196	28	52	12	180	1987년 06월 15일
37	보우덴	2016	두산	3.80	742	159	17	54	6	160	NaN
43	샘슨	2018	한화	4.68	703	144	17	79	5	195	NaN
45	세든	2013	SK	2.98	780	169	14	73	11	160	NaN
48	소사	2012	KIA	3.54	614	137	9	39	8	104	NaN
67	웨버	2014	NC	4.58	512	132	13	42	3	85	NaN
103	윌슨	2018	LG	3.07	689	158	11	35	6	149	1989년 09월 25일
75	탈보트	2012	삼성	3.97	584	136	8	54	5	68	NaN
79	팻딘	2017	KIA	4.14	770	211	22	39	16	143	NaN
82	피가로	2015	삼성	3.38	688	154	16	51	7	117	NaN
84	피어밴드	2015	넥센	4.67	774	202	23	61	12	137	NaN
88	해커	2013	NC	3.63	744	163	12	50	17	127	NaN
97	헥터	2016	KIA	3.40	868	211	7	51	6	139	NaN
100	후랭코프	2018	두산	3.74	621	118	12	55	22	134	1988년 08월 27일

먼저 TBF의 중앙값과 ERA의 중앙값을 pd.Series.median() 함수를 통해 계산해 각각 변수 에 저장
그러고 나서 pd.DataFrame.query() 함수를 통해 데이터프레임 내에서 TBF 중앙값 이상이면서 ERA 중앙값보다 낮은 기록을 추출
해당 과정을 통해 총 18명의 투수 기록이 추출됐습니다 18명의 투수는 성적이 유효하게 우수한 투수
TBF 기록이 특정 횟수보다 높은 투수들을 추출해 투수 기록의 유효성을 확보했고, ERA를 특정 지표보다 낮은 투수들을 추출해 투구 실력의 우수성을 확보
다음 절에서는 해당 투수들의 데이터를 활용해 평균자책점과 제구력과의 관계를 분석하고 스카우팅 모델을 구축해 봄

모델 구축과 검증📑

투수 영입의 목적은 좋은 성적을 낼 투수를 영입하는 것임
- 투수 개인의 능력이 뛰어날수록 좋은 성적을 냄
- 따라서 해당 능력을 객관적으로 평가하는 지표가 필요
- 모델은 정형화된 프로세스이며 함수와 같기때문에 값이 주어졌을 때 정해진 하나의 값을 반환 하는 모델
이번 절에서는 MLB 데이터가 주어졌을 때 투수의 능력을 평가하는 제구력 지표와 아웃 확률을 산출하는 모델을 만들 예정
해당 지표를 통해 투수들의 순위 를 매긴 후 순위가 가장 높은 투수를 영입하는 프로세스를 구축함

1. 선형회귀분석

데이터 전처리 파트에서 TBF 중앙값과 ERA 중앙값을 활용해 KBO에서 유효하면서도 우수한 활약을 보인 투수를 선정함
이번에는 해당 투수들이 KBO에 입성 전 MLB에서 가지고 있던 특성을 선형회귀분석을 통해 밝혀낼 것임
MLB의 데이터는 스카우팅 시점에 확인이 가능한 데이터이므로 해당 데이터를 활용해 투수의 능력을 평가하고 순위를 매길 수 있음
탐색적 데이터 분석 파트에서 확인했듯이, MLB 데이터는 연도별 통계 지표와 투구별 지표가 존재
연도별 통계 지표가 기록된 팬그래프 데이터를 활용해 KBO 입성 전 투수의 특성을 밝히는 것은 제한적임
투수의 고유 능력을 대변할 수 있는 지표가 없기 때문
팬그래프 데이터셋에 기록된 지표들은 소속팀의 수비 능력이나 리그 수준 또는 경기장 요인에 영향을 받으므로 투수의 고유 능력을 대표하는 지표로 사용하기에는 제한적임
하지만 투수의 제구력은 외부 요인의 영향을 받지 않는 투수 고유의 능력이라고 볼 수 있음
제구력은 본인 팀의 수비수가 개입하기 전에 평가할 수 있는 요소이므로 투구를 더 객관적으로 평가할 수 있는 지표

스탯캐스트 데이터에는 투구별 데이터가 기록돼 있으므로 해당 데이터를 활용해 제구력을 수치화해 봄

공이 홈 플레이트를 지날 때의 위치를 시각화

import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize = (10,10))
sns.set_style('darkgrid')
sns.scatterplot(data = atKbo_11_18_StatCast.sort_values('pitch_name'), 
                x = 'plate_x', 
                y = 'plate_z', 
                hue = 'pitch_name', 
                alpha = 0.1)
plt.show()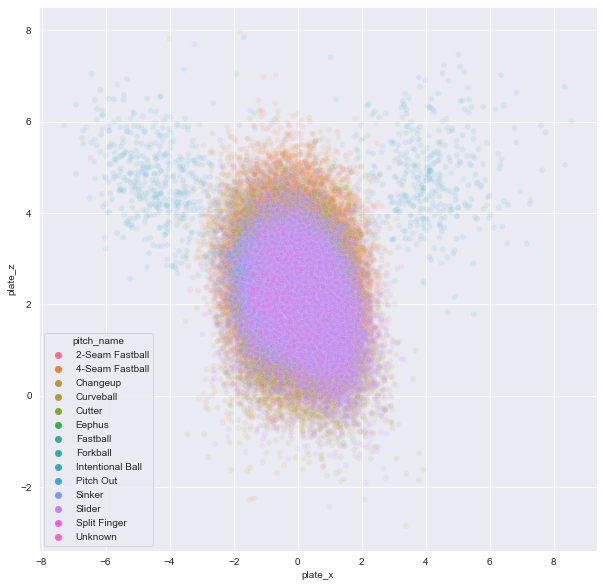

plate_x 칼럼에는 공이 홈 플레이트를 지날 때의 수평 위치가 기록되어 있으며 plate_z 칼럼에는 공이 홈 플레이트를 지날 때의 수직 위치가 기록되어 있음
해당 값들을 Seaborn 라이브러리에서 제공하는 scatterplot 함수를 사용해 좌표 평면에 나타내면 위와 같은 그림이 산출됨
단순히 투구의 좌표 위치만 기록돼 있어 상대적으로 스트라이크 존에서 얼마 나 멀리 있는지 가늠하기가 어려움

스트라이크 존을 함께 시각화
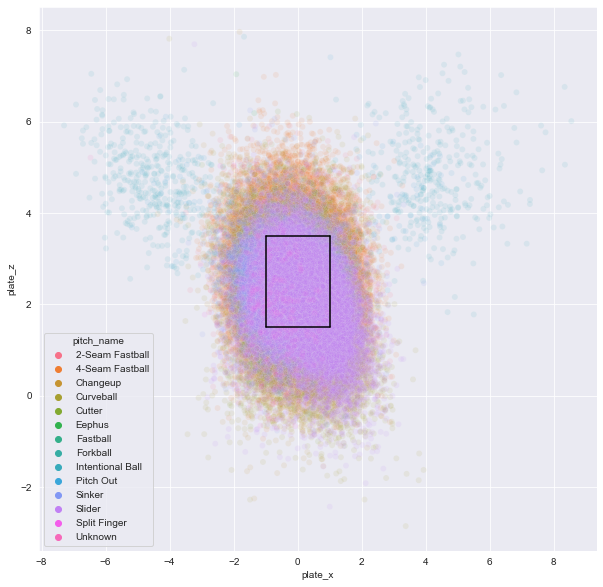
스탯캐스트에서 공식적인 스트라이크 존의 좌표 범위를 공지는 되어 있지 않지만 각종 야구 커뮤니티에서는 스트라이크 존의 범위를 x축 -1에서 1 사이, y축 1.5에서 3.5 사이로 추정하므로 해당 좌표를 기준으로 스트라이크 존을 시각화함
모든 투구를 시각화했기 때문에 스트라이크 존에서 상당히 벗어난 투구가 있는 것을 확인 가능
고의 사구나 피치아웃은 투구 특성상 스트라이크 존에서 많이 벗어나기 때문임
스탯캐스트의 description 칼럼에는 투구별 결과가 기록

그중 스트라이크인 called_strike 투구만 관심을 갖고 앞에서 스트라이크 존 가장자리에 있는 called_strike된 투구가 모든 투수가 목표로 하는 투구라고 가정했기 때문

called_strike 투구만 시각화

plt.figure(figsize = (10,10))
sns.set_style('darkgrid')
sns.scatterplot(data = (atKbo_11_18_StatCast.
                        sort_values('pitch_name').
                        query('description == "called_strike"')), 
                x = 'plate_x', 
                y = 'plate_z', 
                hue = 'pitch_name', 
                alpha = 0.1)
plt.plot([-1, -1], [1.5, 3.5], 'black')
plt.plot([1, 1], [1.5, 3.5], 'black')
plt.plot([-1, 1], [1.5, 1.5], 'black')
plt.plot([-1, 1], [3.5, 3.5], 'black')
plt.show()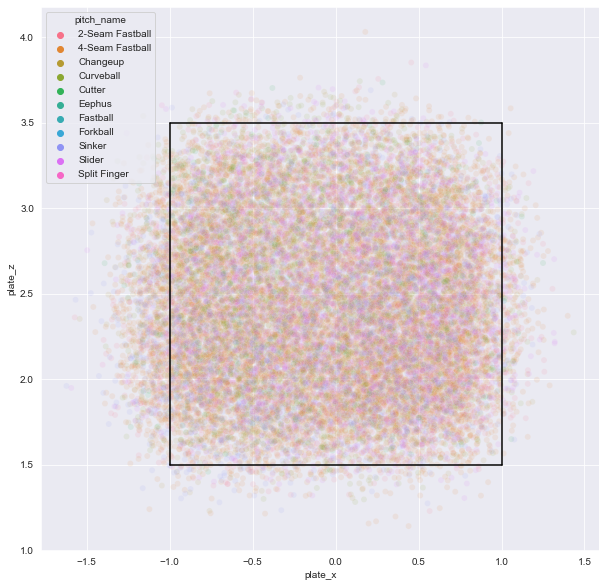

스트라이크인 투구만 추출해 시각화해 보니 임의로 정의한 스트라이크 존 내부에 대부분 투구가 위치한 것을 알 수 있음
정확한 스트라이크 존의 위치는 타자마다 다를 수 있으므로, 필자가 정의한 검정색 선의 정사각형 바깥 부분에도 스트라이크 판정된 공이 존재
필자는 이 투구들 중에서도 스트라이크 존 가장자리에 있는 투구들이야 말로 제구력이 잘 반영된 투구라고 정의함
해당 투구 중에서는 궤적이 스트라이크 존 밖으로 위치할 것처럼 날아오다가 마지막에 변화여 스트라이크 존에 걸친 투구들이 포함됐을 것임

이런 투구들이 투수가 목표로 하는 투구라고 가정했으며, 그렇게 던질 수 있는 구종이 많을수록 제구력이 높을 것이라고 가정함

가장자리에 있는 투구들을 시각화

edgePitches = \
(atKbo_11_18_StatCast.query(
'(plate_x >= 0.8 & plate_x <= 1.2 & plate_z <= 3.7 & plate_z >= 1.3) | \
 (plate_x <= -0.8 & plate_x >= -1.2 & plate_z <= 3.7 & plate_z >= 1.3) | \
 (plate_x >= -0.8 & plate_x <= 0.8 & plate_z <= 1.7 & plate_z >= 1.3) | \
 (plate_x >= -0.8 & plate_x <= 0.8 & plate_z <= 3.7 & plate_z >= 3.3)').
               query('pitch_name.notnull()', engine='python').
               query('description == "called_strike"'))
  
plt.figure(figsize = (10,10))
sns.set_style('darkgrid')
sns.scatterplot(data = edgePitches,
                x = 'plate_x', 
                y = 'plate_z', 
                hue = 'pitch_name', 
                alpha = 0.1)
plt.plot([-1, -1], [1.5, 3.5], 'black')
plt.plot([1, 1], [1.5, 3.5], 'black')
plt.plot([-1, 1], [1.5, 1.5], 'black')
plt.plot([-1, 1], [3.5, 3.5], 'black')
plt.show()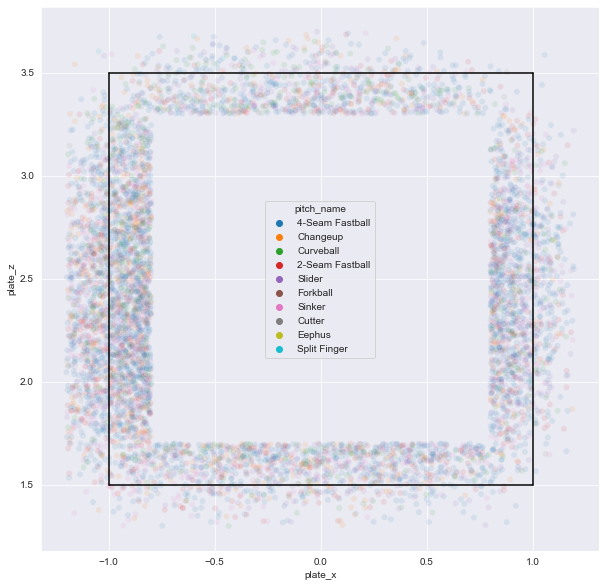

우선 가장자리에 대한 정의를 내려보면 측면당 스트라이크 존 크기의 20%만큼 가장자리를 부여함
- 스트라이크 존의 가로 세로 길이가 2대 2 정사각형이므로 측면당 0.2만큼 씩 더하고 차감함으로써 가장자리를 정의내림
- 그리고 해당 범위에 속하는 called_strike투구들을 추출해 edgePitches 변수에 저장함
- 이때 pitch_name 칼럼에 결측치가 존재하는 경우는 삭제함
- 그 이유는 추후 구종별 비율을 산출할 텐데, 결측값이 포함돼 있으면 비율 산정에 영향을 미치기 때문

제구력은 투수를 객관적으로 평가할 수 있는 요소라고 소개함

이러한 요소를 측정하기 위해서는 추가 정의가 필요
여기서는 제구력을 측정하기 위해 가장자리에 분포한 called_strike된 투구 중 구종 비율이 10%가 넘는 것을 유효한 구종이라고 정의할 것이고, 해당 구종의 개수로 투수의 제구력을 평가할 것임
스트라이크 존 가장자리에 위치 하는 투구 중 우연히 들어온 것도 있을 수 있기에 10% 조건을 주어 배제
정의한 조건에 해당하는 구종의 개수가 많다는 것은 그만큼 제구력이 뛰어나다고도 볼 수 있기에 해당 방 법을 사용

가장자리에 위치한 구종별 투구 수 산출

(edgePitches[['pitcher_name', 'pitch_name', 'game_date']].
 groupby(['pitcher_name', 'pitch_name']).
 count().
 head(10))

		game_date
pitcher_name	pitch_name
니퍼트	2-Seam Fastball	1
	4-Seam Fastball	18
	Changeup	3
	Curveball	3
다이아몬드	2-Seam Fastball	7
	4-Seam Fastball	155
	Changeup	10
	Curveball	36
듀브론트	2-Seam Fastball	80
	4-Seam Fastball	194

가장자리 투구 정보가 저장된 edgePitches 변수로부터 필요한 칼럼들만 추출
pitcher_name과 pitch_name 칼럼은 그룹핑을 하기 위한 기준 칼럼이고, game_date는 투구 개수를 산출하기 위한 더미 칼럼
그다음, pitcher_name과 pitch_name 기준으로 groupby를 실시한 후 count 함수를 사용하면 투수별 구종의 개수가 산출

여기에서 산출된 개수는 edgePitches에 기록된 스트라이크 존 가장자리에 있는 투구 중 called_strike 된 것들만 산출한 것임을 다시 한번 강조

투구들의 상대적인 비율을 산출

(edgePitches[['pitcher_name', 'pitch_name', 'game_date']].
 groupby(['pitcher_name', 'pitch_name']).
 count().
 groupby('pitcher_name').
 apply(lambda x: x / x.sum()).
 head(10))

		game_date
pitcher_name	pitch_name
니퍼트	2-Seam Fastball	0.040000
	4-Seam Fastball	0.720000
	Changeup	0.120000
	Curveball	0.120000
다이아몬드	2-Seam Fastball	0.033654
	4-Seam Fastball	0.745192
	Changeup	0.048077
	Curveball	0.173077
듀브론트	2-Seam Fastball	0.209424
	4-Seam Fastball	0.507853

count 함수를 사용해 투수별 구종 개수를 산출한 후 groupby를 pitcher_name에 대해 한 번 더 실시
그러고 나서 apply 함수를 사용해 구종별 투구 개수를 가장자리에 있는 전체 투구의 합으로 나눔으로써 상대적인 비율을 구함
예를 들어 니퍼트는 2-Seam Fastball을 1 번 던졌고 가장자리에는 총 25개의 투구가 기록
- 따라서 전체 투구에 대한 2-Seam Fastball의 비중은 1/25을 계산해 0.04가 산출

산출된 비율에서 10% 이상인 구종만 추출하고자 함

왜냐하면 던진 비중이 10% 이하인 구종은 우연으로 제구 가 좋게 산출된 구종이라고 정의내렸기 때문

10% 이상인 구종만 추출

(edgePitches[['pitcher_name', 'pitch_name', 'game_date']].
 groupby(['pitcher_name', 'pitch_name']).
 count().
 groupby('pitcher_name').
 apply(lambda x: x / x.sum()).
 query('game_date >= 0.1').
 head(10))

		game_date
pitcher_name	pitch_name
니퍼트	4-Seam Fastball	0.720000
	Changeup	0.120000
	Curveball	0.120000
다이아몬드	4-Seam Fastball	0.745192
	Curveball	0.173077
듀브론트	2-Seam Fastball	0.209424
	4-Seam Fastball	0.507853
	Changeup	0.107330
	Curveball	0.102094
레나도	4-Seam Fastball	0.631579

query 함수를 적용해서 game_date 칼럼 기준 0.1 이상만 추출
현재 game_date 칼럼에는 구종별 투구 비중이 들어 있기 때문

위와 같이 추출된 데이터에 대해 투수별 행의 개수를 구하면 투수별 제구력을 평가하는 지표가 완성됨

투수별 제구력을 평가하는 지표 완성

coordEdge = (edgePitches[['pitcher_name', 'pitch_name', 'game_date']].
             groupby(['pitcher_name', 'pitch_name']).
             count().
             groupby('pitcher_name').
             apply(lambda x : x / x.sum()).
             query('game_date >= 0.1').
             groupby('pitcher_name').
             count())
  
coordEdge = coordEdge.reset_index().rename(columns={'game_date':'num_pitches'})
  
coordEdge.head()

	pitcher_name	num_pitches
0	니퍼트	3
1	다이아몬드	2
2	듀브론트	4
3	레나도	2
4	레온	2

투구 비중이 0.1 이상인 구종들을 추출한 데이터셋에서 pitcher_name 기준으로 groupby를 한 후 count 함수를 사용해 행의 개수를 산출
이렇게 산출된 결과물을 coordEdge라는 변수에 저장한 후 index값을 초기화하고 칼럼명을 game_date에서 num_pitches로 바꿈
최종 결과물을 coordEdge.head()를 통해 확인
정의한 조건에 따라 니퍼트가 제어 가능한 구종은 3개고 다이아몬드는 2개
- 이는 투수별 제구력을 평가하는 지표이며, 높을수록 좋은 수치

산출한 제구력에 따라 KBO에서의 평균자책점이 어떻게 변하는 지 확인

제구력과 KBO에서의 평균자책점

Elite_11_18 = Elite_11_18.reset_index()
  
Elite_11_18 = Elite_11_18.merge(coordEdge, on='pitcher_name')
  
Elite_11_18.boxplot('ERA', 'num_pitches')
  
# 실행 결과
<AxesSubplot:title={'center':'ERA'}, xlabel='num_pitches'>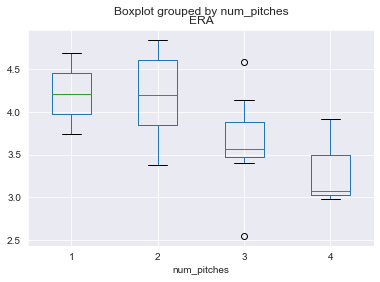

Elite_11_18에는 데이터 전처리 파트에서 추출한 투수들의 정보가 저장돼 있음.
- 해당 투수들은 국내 리그에서 유효한 우수 성적을 보여준 투수들
인덱스 값이 현재 정돈되어 있지 않으므로 reset_index함수를 통해 정리해줌
그 후 해당 투수들에 대한 제구력 지표를 merge 함수를 통해 추가함
그러고 나서 boxplot 함수를 통해 상자그림으로 시각화함
출력물을 확인하면 제구력이 높아질수록 평균자책점이 감소하는 것을 볼 수 있음

이러한 경향이 통계적으로도 유의한지 검증하기 위해 선형회귀분석 을 실시합니다.

선형회귀분석

import statsmodels.api as sm
  
y = Elite_11_18.ERA.values
X = sm.add_constant(Elite_11_18.num_pitches.values)
  
model = sm.OLS(y, X)
  
result = model.fit()
  
result.summary()

OLS Regression Results

Dep. Variable:	y	R-squared:	0.268
Model:	OLS	Adj. R-squared:	0.222
Method:	Least Squares	F-statistic:	5.861
Date:	Fri, 15 Apr 2022	Prob (F-statistic):	0.0277
Time:	08:16:12	Log-Likelihood:	-14.248
No. Observations:	18	AIC:	32.50
Df Residuals:	16	BIC:	34.28
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
const	4.7731	0.414	11.543	0.000	3.896	5.650
x1	-0.3629	0.150	-2.421	0.028	-0.681	-0.045

Omnibus:	0.141	Durbin-Watson:	1.946
Prob(Omnibus):	0.932	Jarque-Bera (JB):	0.346
Skew:	-0.120	Prob(JB):	0.841
Kurtosis:	2.365	Cond. No.	9.56

이 분석에서 종속변수는 KBO 첫 시즌에서의 평균자책점이며 독립변수는 투수의 제구력임
- 따라서 Elite_11_18 데이터에서 ERA 칼럼의 값들을 y 변수에 저장하고 num_pitches 칼럼의 값들을 X 변수에 저장
- 단순 선형회귀 모델은 형태로 구성돼 있으므로 상수항을 더하기 위해 add.constant 함수를 사용
- 그러고 나서 선형회귀 모델을 OLS 함수를 통 해 정의하고 fit 함수를 통해 모델 훈련을 진행
- 마지막으로 summary 함수를 통해 선 형회귀분석 결과 리포트를 출력
독립변수인 x1의 계수가 -0.3629로 계산됨
- 이는 제구력 지표가 1 상승할 때마다 KBO에서의 ERA가 평균적으로 0.3629만큼 감소한다고 해석 가능
- 해당 계수의 p-value가 0.028으로 0.05보다 작으므로 유의한 결과가 나왔다고 해석 가능
- 과거 데이터에 대해 선형회귀분석을 통해 얻은 유의한 인사이트를 바탕으로 2019년 외국인 투수를 스카우팅할 때도 제구력을 평가해 그 점수가 가장 높은 투수를 스카우팅하고자 함

2. 아웃 확률 추정하기

앞서 제구력 지표를 확인했지만 제구력이 동점으로 나올 수도있음
대회의 목표는 스카우팅하고자 하는 2명의 투수를 제시하는 것인데, 제구력 점수가 동점인 선수가 3명 이상이 나오는 경우 추가 선발 기준이 필요
해당 기준으로는 아웃 확률 을 사용
- 여기에서 정의하고자 하는 아웃 확률은 1996년에 발표된 “Modeling Pitcher Performance and the Distribution of Runs per Inning in Major League Baseball” 논문에 나오는 개념을 뜻함
- 아웃 확률은 투수가 한 이닝에 상대하는 타자의 수가 따르는 음이항 분포에서 나오는 모수임
- 음이항 분포를 설명하기 위해 이항분포를 먼저 소개함
이항분포는 두 가지 배반사건이 나오는 싱황에서 n번의 시행 횟수 내에 특정 사건이 성공한 건 수를 모델링할 때 쓰는 분포
- 예를 들어, 3번 동전을 던졌을 때 나오는 앞면의 수의 확률 값이 궁금할 때 이항분포를 사용
- 즉, 동전을 던지는 시행 횟수는 고정돼 있고, 앞면이 나오는 특정 사건의 성공 횟수는 유동적임
- 그러므로 특정 사건의 성공 횟수가 확률 변수가 됨

음이항 분포는 이것의 정반대

특정 사건의 성공 횟수가 고정돼있고, 해당 성공 횟수를 달성하기까지 시행한 횟수가 확률변수에 대응
예를 들어, 3개의 앞면이 나오기까지 동전을 던진 횟수를 모델링할 때 음이항 분포를 사용

이항 분포와 음이항 분포

이항분포	음이항분포
X~B(n, p)	X~NB(k, p)
동전 던지기에서 3번 동전을 던졌을 때 나온 앞면의 수 = X 〜B(3, 0.5)(0 ≤ X ≤ 3) n： 시행 횟수 (고정) X：n번의 시행 횟수 내에서, 해당사건이 발생한 건수	동전 던지기에서 3번의 앞면이 나오기 위해서 동전을 던진 횟수 = X~NB(3, 0.5) (3 ≤ X) k： 성공 횟수 (고정) X： 해당 사건이 k번 발생하기까지 시행한 횟수

그렇기에 음이항 분포는 투수의 활약상을 모델링하기에 아주 적합한 분포
투수는 한 이닝에서 3번의 아웃을 잡기 위해 타자를 계속 상대하게 됨
그러므로 3개의 아웃을 잡을 때까지 상대한 타자의 수가 확률변수 X인 음이항 분포를 만들 수 있음

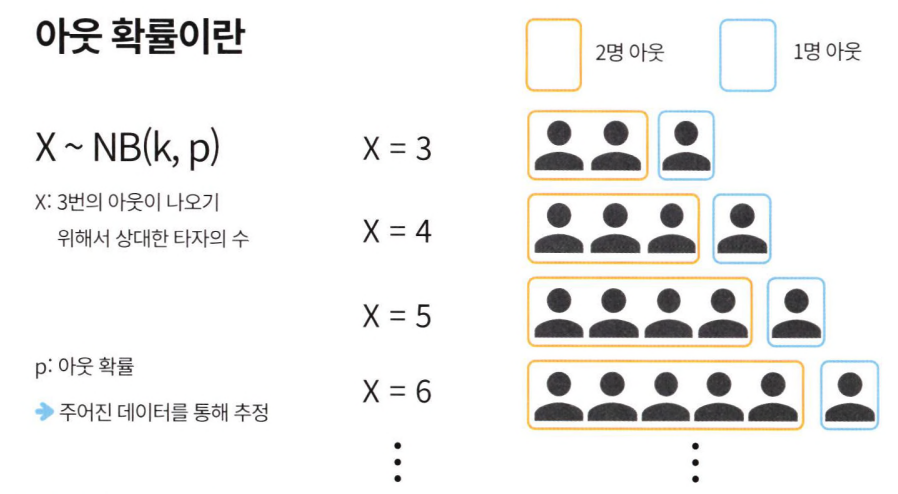
k가 3인 음이항 분포 예시
예를 들어, X가 3이라는 말은 연속적으로 세 명의 타자를 아웃시켰다는 뜻이고, X가 4라면 처음 마주한 3명의 타자 중 2명을 아웃시키고, 4번째 타자를 아웃시켰다는 뜻임
여기서 3개의 아웃은 한 이닝이 끝나는 시점을 의미하므로 한 이닝 끝날 때까지 투수가 상대한 타자의 수를 모델링할 때 사용할 수 있는 분포
여기서 모수 p는 투수가 한 명의 타자를 아웃시킬 확률을 뜻함
이 확률을 추정하기 위해서는 한 이닝이 끝날 때까지 투수가 상대한 타자의 수에 대한 데이터가 필요함
해당 데이터는 스탯캐스트 데이터를 가공해 도출해 낼 수 있음

투수가 이닝별로 상대한 타자의 수를 도출하는 방법은 다음과 같음

스탯캐스트 데이터의 events 칼럼에는 타석별 결과가 기록되어 있음
타석별 오직 하나의 결과만 기록되며 나머지에는 모두 결측값이 입력돼 있음
그러므로 events 칼럼에 결측값이 포함된 행을 제거하면 투수별로 해당 경기에 상대한 고유 타자들만 남게 됨
이어지는 두 코드를 통 해 해당 과정을 확인해 봄
우선, 스탯캐스트 데이터의 events 칼럼 값을 확인

스탯캐스트 데이터의 events 칼럼 값

atKbo_11_18_StatCast[['batter', 'events', 'description']].head(10)

	batter	events	description
0	425834.0	field_out	hit_into_play
1	150289.0	home_run	hit_into_play_score
2	150289.0	NaN	foul
3	150289.0	NaN	blocked_ball
4	150289.0	NaN	ball
5	150289.0	NaN	foul_tip
6	150289.0	NaN	ball
7	430632.0	field_out	hit_into_play
8	430632.0	NaN	ball
9	430632.0	NaN	ball

경기 진행에 따른 투구 결과가 스탯캐스트 데이터에는 아래에서 위로 기록
그렇기 때문에 아래에서 위 순서로 events에 값이 기록될 때마다 다음 행의 batter 값이 바뀐 것을 확인 가능

events 칼럼의 결측값을 모두 제거하고 문자열만 남김

events 칼럼의 결측값을 제거

(atKbo_11_18_StatCast[['batter', 'events', 'description']].
 query('events.notnull()', engine='python').
 head(10))

	batter	events	description
0	425834.0	field_out	hit_into_play
1	150289.0	home_run	hit_into_play_score
7	430632.0	field_out	hit_into_play
10	446481.0	single	hit_into_play_no_out
12	446334.0	field_out	hit_into_play
15	116338.0	field_out	hit_into_play
19	110029.0	field_out	hit_into_play
25	435062.0	field_out	hit_into_play
29	488721.0	home_run	hit_into_play_score
31	430948.0	field_out	hit_into_play

events 칼럼에 결측값이 있는 행을 모두 제거해 고유 batter의 정보만 남음
해당 과정을 통해 투수가 해당 경기에 상대한 고유 타자 수를 알 수 있음.

이닝별 상대 타자 수를 산출하기 위해서는 해당 데이터를 순차적으로 순회하면서 직접 카운팅해야 함

이닝별 상대 타자 수를 산출

def recordInning(key, dic):    
    if dic.get(key) == None :
        dic[key] = 1
    else :
        dic[key] += 1
      
    return dic
      
  
def getInningResult(df):
    batterCount = 0
    batterCountTemp = 0
    outs = ['out', 'out', 'out']
    inningDict = {}
      
    for idx in range(len(df)-1, -1, -1):
        batterCount += 1
          
        if 'out' in df.events.iloc[idx]:
            outs.pop()
          
        # out이 3번 나오면 기록
        if len(outs) == 0:
            _key = f'I_{batterCount - batterCountTemp}'
            inningDict = recordInning(_key, inningDict)
            batterCountTemp = batterCount
              
            if idx != 0 :
                outs = ['out', 'out', 'out']
              
    if len(outs) != 0:
        _key = f'I_{batterCount - batterCountTemp + len(outs)}'
        inningDict = recordInning(_key, inningDict)
      
    return pd.DataFrame(data = dict(sorted(inningDict.items())), index = [0])

해당 알고리즘은 스탯캐스트 데이터를 아래에서 위로 순회할 때마다 batterCount를 증가시킴
- 그리고 events 칼럼에 기록된 문자열 값 중 out이 포함된 events를 만나면 outs 리 스트에서 out문자열을 하나 제거
- outs리스트가 빈 상태가 되면 3번의 out이 나온 것임
- 이때, 상대한 타자 수가 N이라고 하면 I_N 키 값에 1을 증가시킴
- 마지막 행인 idx값 0에 도달하지 않았다는 것은 아직 해당 경기의 투구 기록이 남아 있다는 것이므로 outs 리스트를 초기화하고 순회 작업을 반복함
투수가 중도 교체될 경우 outs 리스트에는 out 문자열이 남아 있을 것임
해당 이닝을 마 무리하지 못했으므로 교체되기 전까지 상대한 타자 수에 남은 아웃 카운트 개수를 더해 상대 한 타자 수를 추정

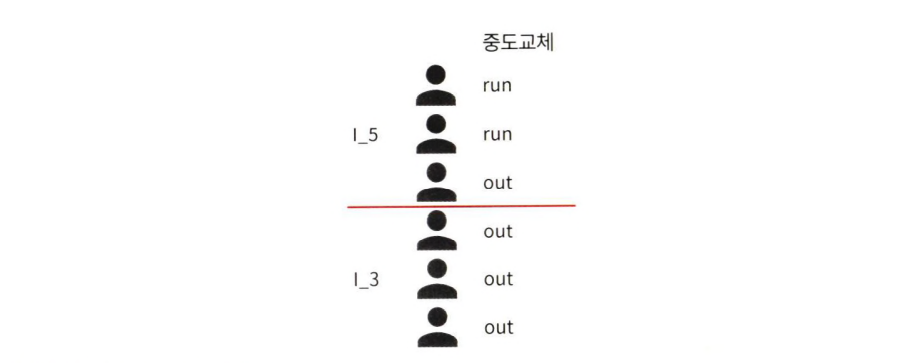
이닝별 상대한 타자 예시
위의 그림을 통해 예를 들어보면, 첫 번째 이닝에서 3명 의 타자를 상대했으므로 I_3에 기록하고 두 번째 이닝에서 한 명을 아웃시키고 두 명을 출루 시켜 중도 교체를 당했다면, outs 리스트에는 2개의 out이 남게 됨

그래서 두 번째 이닝 은 총 5명을 상대했다고 추정하고 I_5에 기록

함수의 실행 결과를 확인

MLB_11_18_InningSummary = (atKbo_11_18_StatCast.query('events.notnull()',
                                                      engine='python').
                           groupby(['pitcher_name', 'game_date']).
                           apply(getInningResult))
  
MLB_11_18_InningSummary.head()

			I_6	I_7	I_4	I_5	I_8	I_3	I_12	I_10	I_9	I_11	I_14	I_13	I_17	I_16
pitcher_name	game_date
니퍼트	2010-06-06	0	2.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-06-09	0	NaN	1.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-06-17	0	NaN	NaN	1.0	1.0	1.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-06-23	0	1.0	1.0	1.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-06-30	0	1.0	NaN	1.0	NaN	NaN	1.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

getlnningResult 함수를 적용하기 전에 events 칼럼에 결측값이 있는 경우를 먼저 제거
- pitcher_name, game_date 기준으로 스탯캐스트 데이터를 groupby 한 후 getlnningResult 함수를 적용
- 투수의 경기별 이닝 결과가 산출돼 줄력됨
- 예를 들어 니퍼트는 2010년 6월 6일 경기에서 2개의 이닝 동안 각각 6명의 타자를 상대 했으며 6월 9일 경기에서는 하나의 이닝 동안 7명의 타자를 상대했음을 알 수 있음

해당 결과물을 pitcher_name 기준으로 groupby를 실시한 후 칼럼별 합을 구하면 투수별 MLB에서의 모든 경기 기록이 합산됨

투수별 MLB에서의 모든 경기 가록 합산

MLB_11_18_InningSummary = (MLB_11_18_InningSummary.
                           groupby('pitcher_name').
                           sum()[sorted(MLB_11_18_InningSummary.columns)])
  
MLB_11_18_InningSummary.head()

	I_10	I_11	I_12	I_13	I_14	I_16	I_17	I_3	I_4	I_5	I_6	I_7	I_8	I_9
pitcher_name
니퍼트	0.0	0.0	1.0	0.0	0.0	0.0	0.0	8.0	14.0	2.0	6.0	3.0	1.0	0.0
다이아몬드	6.0	1.0	0.0	0.0	1.0	0.0	0.0	105.0	65.0	60.0	33.0	25.0	22.0	6.0
듀브론트	9.0	1.0	1.0	0.0	0.0	0.0	0.0	146.0	150.0	79.0	63.0	29.0	26.0	14.0
레나도	0.0	1.0	0.0	0.0	0.0	0.0	0.0	26.0	25.0	15.0	9.0	10.0	3.0	1.0
레온	0.0	0.0	0.0	0.0	0.0	0.0	0.0	7.0	6.0	6.0	4.0	3.0	1.0	0.0

groupby 함수를 통해 투수별로 묶어준 후 sum 함수를 통해 칼럼별 합을 구함
마지막으 로 칼럼 순서를 정렬해 출력하면 위와 같은 결과가 나옴
결과를 해석하자면, 니퍼트는 MLB에서 3명의 타자를 상대한 이닝을 8번 겪었고, 4명의 타자를 상대한 이닝을 14번 겪었으며, 5명의 타자를 상대한 이닝을 2번 겪은 것을 알 수 있음

다음으로, 전체 투수 중 Elite_11_18에 기록된 투수들에 대한 정보만 추출해 봄

Elite_11_18에 기록된 투수들에 대한 정보만 추출

MLB_11_18_InningSummary = MLB_11_18_InningSummary.reset_index()
  
Elite_11_18_InningSummary = (MLB_11_18_InningSummary.
                             query('pitcher_name in @Elite_11_18.pitcher_name').
                             reset_index(drop = True))
  
Elite_11_18_InningSummary

	pitcher_name	I_10	I_11	I_12	I_13	I_14	I_16	I_3	I_4	I_5	I_6	I_7	I_8	I_9
0	니퍼트	0.0	0.0	1.0	0.0	0.0	0.0	8.0	14.0	2.0	6.0	3.0	1.0	0.0
1	다이아몬드	6.0	1.0	0.0	0.0	1.0	0.0	105.0	65.0	60.0	33.0	25.0	22.0	6.0
2	레이예스	0.0	0.0	0.0	0.0	0.0	0.0	34.0	43.0	24.0	17.0	10.0	9.0	5.0
3	레일리	0.0	0.0	0.0	0.0	0.0	0.0	11.0	12.0	6.0	6.0	1.0	3.0	2.0
4	린드블럼	0.0	0.0	0.0	0.0	0.0	0.0	54.0	41.0	35.0	15.0	9.0	2.0	1.0
5	보우덴	0.0	0.0	0.0	0.0	0.0	0.0	37.0	49.0	12.0	21.0	6.0	2.0	1.0
6	샘슨	1.0	0.0	0.0	0.0	0.0	0.0	23.0	21.0	13.0	20.0	8.0	5.0	2.0
7	세든	0.0	0.0	0.0	0.0	0.0	0.0	24.0	13.0	11.0	6.0	4.0	3.0	1.0
8	소사	1.0	1.0	0.0	0.0	0.0	0.0	17.0	5.0	11.0	11.0	2.0	2.0	0.0
9	웨버	0.0	0.0	0.0	0.0	0.0	0.0	4.0	4.0	3.0	4.0	2.0	2.0	0.0
10	윌슨	0.0	0.0	1.0	0.0	0.0	0.0	42.0	38.0	24.0	22.0	9.0	6.0	4.0
11	탈보트	1.0	1.0	3.0	1.0	0.0	0.0	30.0	39.0	28.0	24.0	9.0	7.0	6.0
12	팻딘	0.0	0.0	0.0	0.0	0.0	1.0	17.0	16.0	10.0	10.0	9.0	1.0	1.0
13	피가로	0.0	0.0	0.0	0.0	0.0	0.0	31.0	22.0	28.0	12.0	5.0	3.0	1.0
14	피어밴드	0.0	0.0	0.0	0.0	0.0	0.0	2.0	4.0	2.0	0.0	1.0	1.0	0.0
15	해커	0.0	0.0	0.0	0.0	0.0	0.0	3.0	2.0	6.0	2.0	1.0	1.0	0.0
16	헥터	6.0	4.0	0.0	0.0	0.0	0.0	123.0	96.0	75.0	44.0	33.0	9.0	7.0
17	후랭코프	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0	1.0	0.0	0.0	0.0

총 18명 투수의 정보가 추출됨
이제 해당 정보를 바탕으로 투수별 아웃 확률을 산출

이닝별 상대한 타자 수를 바탕으로 아웃 확률을 추정하는 방법은 앞서 언급한 논문에 나와 있으므로 해당 논문에 나온 공식을 구현

투수별 아웃 확률을 산출하는 함수

def makeC1(df):
    '''
    Parameters:
    -----------
    df: InningSummary
      
    Returns:
    --------
    pd.Series
        논문에서 정의한 C1 값
    '''
    return df.sum(axis = 1)
  
def makeC2(df):
    '''
    Parameters:
    -----------
    df: InningSummary
      
    Returns:
    --------
    pd.Series
        논문에서 정의한 C2 값
    '''
    return 3*(df['I_3'] + df['I_4'])
  
def makeC3(df):
    '''
    Parameters:
    -----------
    df: InningSummary
      
    Returns:
    --------
    pd.Series
        논문에서 정의한 C3 값
    '''
    output = 0
    for N in range(5,18):
        try:
            output += (N-3)*df[f'I_{N}']
        except:
            continue
    return output
  
def makeDelta(df):
    '''
    Parameters:
    -----------
    df: InningSummary with C1, C2, C3
      
    Returns:
    --------
    pd.Series
        논문에서 정의한 Delta 값
    '''
    Delta = ((-df['C1'] + df['C2'] + 2*df['C3']) + 
             ((df['C1'] - df['C2'] - 2*df['C3']).pow(2) + 
              4*df['C3']*(3*df['C1'] + df['C2'] + 3*df['C3'])).pow(0.5)) / \
    (2*(3*df['C1'] + df['C2'] + 3*df['C3']))
    return Delta
  
def makeOutProb(df):
    '''
    Parameters:
    -----------
    df: InningSummary
      
    Returns:
    --------
    pd.DataFrame
        InningSummary with C1, C2, C3, Delta, outProb
    '''
    df['C1']=makeC1(df)
    df['C2']=makeC2(df)
    df['C3']=makeC3(df)
  
    df['Delta'] = makeDelta(df)
    df['outProb'] = 1 - df['Delta']
      
    return df

makeOutProb 함수를 사용하면 아웃 확률이 추정되므로 아웃 확률을 산출

Elite_11_18_InningSummary = makeOutProb(Elite_11_18_InningSummary)
Elite_11_18_InningSummary.sort_values('outProb', ascending = False)

	pitcher_name	I_10	I_11	I_12	I_13	I_14	I_16	I_3	I_4	I_5	I_6	I_7	I_8	I_9	C1	C2	C3	Delta	outProb
5	보우덴	0.0	0.0	0.0	0.0	0.0	0.0	37.0	49.0	12.0	21.0	6.0	2.0	1.0	128.0	258.0	127.0	0.586895	0.413105
4	린드블럼	0.0	0.0	0.0	0.0	0.0	0.0	54.0	41.0	35.0	15.0	9.0	2.0	1.0	157.0	285.0	167.0	0.591972	0.408028
7	세든	0.0	0.0	0.0	0.0	0.0	0.0	24.0	13.0	11.0	6.0	4.0	3.0	1.0	62.0	111.0	77.0	0.619771	0.380229
13	피가로	0.0	0.0	0.0	0.0	0.0	0.0	31.0	22.0	28.0	12.0	5.0	3.0	1.0	102.0	159.0	133.0	0.621519	0.378481
14	피어밴드	0.0	0.0	0.0	0.0	0.0	0.0	2.0	4.0	2.0	0.0	1.0	1.0	0.0	10.0	18.0	13.0	0.628539	0.371461
0	니퍼트	0.0	0.0	1.0	0.0	0.0	0.0	8.0	14.0	2.0	6.0	3.0	1.0	0.0	35.0	66.0	48.0	0.640926	0.359074
16	헥터	6.0	4.0	0.0	0.0	0.0	0.0	123.0	96.0	75.0	44.0	33.0	9.0	7.0	397.0	657.0	575.0	0.644372	0.355628
10	윌슨	0.0	0.0	1.0	0.0	0.0	0.0	42.0	38.0	24.0	22.0	9.0	6.0	4.0	146.0	240.0	213.0	0.645420	0.354580
3	레일리	0.0	0.0	0.0	0.0	0.0	0.0	11.0	12.0	6.0	6.0	1.0	3.0	2.0	41.0	69.0	61.0	0.650185	0.349815
2	레이예스	0.0	0.0	0.0	0.0	0.0	0.0	34.0	43.0	24.0	17.0	10.0	9.0	5.0	142.0	231.0	214.0	0.651042	0.348958
1	다이아몬드	6.0	1.0	0.0	0.0	1.0	0.0	105.0	65.0	60.0	33.0	25.0	22.0	6.0	324.0	510.0	526.0	0.663607	0.336393
15	해커	0.0	0.0	0.0	0.0	0.0	0.0	3.0	2.0	6.0	2.0	1.0	1.0	0.0	15.0	15.0	27.0	0.669148	0.330852
12	팻딘	0.0	0.0	0.0	0.0	0.0	1.0	17.0	16.0	10.0	10.0	9.0	1.0	1.0	65.0	99.0	110.0	0.670114	0.329886
8	소사	1.0	1.0	0.0	0.0	0.0	0.0	17.0	5.0	11.0	11.0	2.0	2.0	0.0	50.0	66.0	88.0	0.672582	0.327418
6	샘슨	1.0	0.0	0.0	0.0	0.0	0.0	23.0	21.0	13.0	20.0	8.0	5.0	2.0	93.0	132.0	162.0	0.673026	0.326974
9	웨버	0.0	0.0	0.0	0.0	0.0	0.0	4.0	4.0	3.0	4.0	2.0	2.0	0.0	19.0	24.0	36.0	0.685338	0.314662
11	탈보트	1.0	1.0	3.0	1.0	0.0	0.0	30.0	39.0	28.0	24.0	9.0	7.0	6.0	149.0	207.0	287.0	0.691225	0.308775
17	후랭코프	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0	1.0	0.0	0.0	0.0	2.0	0.0	5.0	0.714286	0.285714

이렇게 해서 제구력을 평가하는 지표를 산출하고 아웃 확률까지 도출하는 함수가 모두 완성 됨

이제 해당 과정을 2019년도 데이터에 적용해 스카우트하고자 하는 투수를 선발해 봄

2019년도 데이터에 적용

edgePitches_19 = \
(atKbo_19_StatCast.query(
    '(plate_x >= 0.8 & plate_x <= 1.2 & plate_z <= 3.7 & plate_z >= 1.3) | \
     (plate_x <= -0.8 & plate_x >= -1.2 & plate_z <= 3.7 & plate_z >= 1.3) | \
     (plate_x >= -0.8 & plate_x <= 0.8 & plate_z <= 1.7 & plate_z >= 1.3) | \
     (plate_x >= -0.8 & plate_x <= 0.8 & plate_z <= 3.7 & plate_z >= 3.3)').
 query('pitch_name.notnull()', engine='python').
 query('description == "called_strike"'))
  
coordEdge_19 = \
(edgePitches_19[['pitcher_name', 'pitch_name', 'game_date']].
 groupby(['pitcher_name', 'pitch_name']).
 count().
 groupby('pitcher_name').
 apply(lambda x : x / x.sum()).
 query('game_date >= 0.1').
 groupby('pitcher_name').
 count())
  
MLB_19_InningSummary = (atKbo_19_StatCast.query('events.notnull()', engine = 'python').
                        groupby(['pitcher_name', 'game_date']).
                        apply(getInningResult))
  
MLB_19_InningSummary = (MLB_19_InningSummary.
                        groupby('pitcher_name').
                        sum()[sorted(MLB_19_InningSummary.columns)])
  
MLB_19_InningSummary = MLB_19_InningSummary.reset_index()
  
MLB_19_InningSummary = makeOutProb(MLB_19_InningSummary)
MLB_19_InningSummary.sort_values('outProb', ascending=False)

	pitcher_name	I_10	I_11	I_12	I_13	I_15	I_3	I_4	I_5	I_6	I_7	I_8	I_9	C1	C2	C3	Delta	outProb
3	서폴드	0.0	1.0	0.0	0.0	0.0	38.0	31.0	28.0	16.0	7.0	3.0	1.0	125.0	207.0	161.0	0.622278	0.377722
0	루친스키	1.0	0.0	0.0	0.0	0.0	24.0	11.0	14.0	7.0	1.0	3.0	2.0	63.0	105.0	87.0	0.635756	0.364244
5	요키시	0.0	0.0	0.0	0.0	0.0	4.0	3.0	4.0	3.0	0.0	0.0	1.0	15.0	21.0	23.0	0.648073	0.351927
12	헤일리	0.0	0.0	0.0	0.0	0.0	7.0	6.0	8.0	3.0	2.0	2.0	0.0	28.0	39.0	43.0	0.648175	0.351825
6	윌랜드	1.0	0.0	0.0	0.0	0.0	20.0	11.0	6.0	7.0	5.0	3.0	1.0	54.0	93.0	81.0	0.652780	0.347220
10	터너	4.0	3.0	0.0	0.0	1.0	105.0	89.0	71.0	51.0	22.0	16.0	8.0	370.0	582.0	575.0	0.655363	0.344637
1	맥과이어	0.0	0.0	0.0	0.0	0.0	14.0	13.0	9.0	6.0	3.0	3.0	4.0	52.0	81.0	87.0	0.668831	0.331169
4	알칸타라	0.0	0.0	0.0	1.0	0.0	15.0	8.0	8.0	9.0	3.0	3.0	0.0	47.0	69.0	80.0	0.669846	0.330154
8	켈리	1.0	2.0	1.0	0.0	0.0	23.0	20.0	18.0	8.0	9.0	2.0	1.0	85.0	129.0	144.0	0.670181	0.329819
11	톰슨	0.0	0.0	1.0	0.0	0.0	31.0	29.0	15.0	13.0	12.0	7.0	5.0	113.0	180.0	191.0	0.671605	0.328395
2	버틀러	3.0	0.0	4.0	0.0	1.0	72.0	57.0	58.0	31.0	22.0	12.0	5.0	265.0	387.0	456.0	0.671711	0.328289
7	채드벨	1.0	0.0	0.0	0.0	0.0	16.0	17.0	15.0	9.0	10.0	4.0	1.0	73.0	99.0	130.0	0.675697	0.324303
9	쿠에바스	1.0	0.0	0.0	0.0	0.0	2.0	6.0	8.0	4.0	2.0	1.0	0.0	24.0	24.0	48.0	0.689898	0.310102

2019년도 스카우트 대상 투수별 MLB 리그 데이터를 기반으로 아웃 확률이 산출됨

이 중에서 제구력이 가장 뛰어난 선수가 누구인지 확인

제구력이 가장 뛰어난 선수

coordEdge_19 = coordEdge_19.reset_index().rename(columns={'game_date':'num_pitches'})
  
coordEdge_19.sort_values('num_pitches', ascending = False)

	pitcher_name	num_pitches
0	루친스키	4
7	채드벨	4
9	쿠에바스	4
1	맥과이어	3
3	서폴드	3
4	알칸타라	3
5	요키시	3
8	켈리	3
10	터너	3
11	톰슨	3
12	헤일리	3
2	버틀러	2
6	윌랜드	2

2019년도 신입 투수 중 제구력이 가장 높은 투수는 루친스키, 채드벨 쿠에바스임
- 해당 투수 중 최종 2명을 선발하기 위해 아웃 확률을 확인
- 루친스키의 아웃 확률은 0.364, 채드벨은 0.324, 쿠에바스는 0.310이므로, 루친스키와 채드벨을 최종적으로 스카우팅함
이번 예시에서는 투수의 능력을 평가하기 위해 투구의 좌표 데이터만 활용했지만, 그 외에도 스탯캐스트 데이터에 있는 구속 발사 각도, 볼 배합 구조 등을 활용한다면 좀 더 풍부한 인사이트를 발굴할 수 있을 것임

Twitter Facebook LinkedIn

⚾Chapter05 외국인 투수 스카우팅 최적화 2 - 데이터 전처리, 모델 구축과 검증

데이터 전처리📑

1. 가설을 확인하기 위한 투수 집단 선정하기

2. 유효한 데이터 선정하기

모델 구축과 검증📑

1. 선형회귀분석

2. 아웃 확률 추정하기

공유하기

댓글남기기

참고

시간복잡도(time complexity)는 어떻게 계산하는가?

소프트웨어 디자인 패턴(Design Pattern)은 무엇인가?

⚾Chapter05 외국인 투수 스카우팅 최적화 3 - 볼 배합 지표, 배럴 타구 허용 비율

⚾Chapter05 외국인 투수 스카우팅 최적화 1 - 문제 정의, 탐색적 데이터 분석