⚾Chapter01 KBO 타자 OPS 예측 3 - 성능 향상을 위한 방법, 정리

5_ 성능 향상을 위한 방법📑
- 지금까지 2019 KBO 상반기 타자들의 OPS 성적을 예측하기 위한 작업 진행
- 데이터 이해
- 전처리
- 모델링
- 이러한 과정을 적용하면 곧바로 2019 상반기 타자의 예측 OPS 값을 도출 가능
- 하지만 대회 수상을 위해서는 단순히 예측 OPS 값만 도출하는 것 으로는 부족하기에 도출된 예측 OPS 값이 실제 OPS와 유사해야 함
- 예측된 OPS 와 실제 OPS의 수치가 비슷할수록 모델의 성능이 우수하다고 평가
5_1 앙상블
-
모델의 성능 향상을 위해 널리 이용되는 방법
앙상블 -
앙상블은 여러 모델의 결과를 종합해 사용하는 것을 의미- 여러 모델의 예측 결과를 더해 평균을 내면 하나의 모델을 사용하는 것보다 더 좋은 결과를 보일 때가 많음.
- 각 모델의 결론을 종합해 더 보편적인 결과를 이끌어내기 때문
-
이번 대회 역시 앙상블 기법을 이용해 모델의 성능이 더 좋아질 수 있는지 확인
-
보통 서로 다른 알고리즘이면서 비슷한 성능을 보이는 결과를 결합할 때 좋은 성능을 보임
-
릿지회귀 모델과라쏘회귀 모델은 동일한 선형회귀 모델이므로 성능이 좀 더 좋았던 라쏘를 사용하고,XGBoost는 다른 알고리즘에 비해 성능이 좋지 않았으므로라쏘와랜덤 포레스트를 이용해 앙상블을 진행 -
두 모델의 예측값을 평균 내어 테스트 데이터셋 에 적용한 이후 WRMSE의 값을 비교
-
두 모델의 평균을 이용해 앙상블
print('OBP model averaging: ', wrmse(OBP_test['OBP'], OBP_test['AB'], (Lasso_OBP + RF_OBP) / 2)) print('SLG model averaging: ', wrmse(SLG_test['SLG'], OBP_test['AB'], (Lasso_SLG + RF_SLG) / 2))OBP model averaging: 0.33245746520105823 SLG model averaging: 0.6684541138633259 -
두 모델의 평균을 이용해 앙상블한 결과, 출루율은 0.332의 WRMSE 값을 보여주어 정확도가 소폭 하락했지만 장타율은 0.668의 WRMSE 값을 보여 정확도가 소폭 상승
-
앙상블의 성능 향상 효과를 높이려면 모델 간 성능이 비슷해야 하는데 장타율은 라쏘 선형회귀 모델의 성능이 더 좋아서 이런 결과가 나온 것으로 추정 가능
5_2 단순화된 모델 생성
-
앞에서 변수 선택을 진행할 때 각 지표가 서로 높은 상관계수를 지니고 있음을 확인
-
이에 따라 이번 분석에서는 OBP와 SLG의 예측에 가장 중요하다고 생각되는 변수로 OBP와 SLG만 사용
-
하지만 다른 변수를 추가로 이용하지 않는 것이 모델 성능에 정확히 어떤 영향을 미칠지는 알수 없음
-
OBP 예측 모델에 다른 변수들을 포함할 경우 모델의 성능이 어떻게 달라지는지 한번 확인
-
구체적으로 볼넷(BB). 루타(TB), 타점(RBI)을 추가해 모델을 구성했을 때의 결과를 봄
-
여기서 모델은 랜덤 포레스트만 이용하고 과거 1개 연도의 lag 변수만 생성해 결과를 비교
-
다음 과정은 볼넷(BB), 루타(TB), 타점(BRI) 각각의 lag 변수를 만들기 위해 시행한 전처리 코드
-
lag 변수를 만들기 위해 전처리
# 전처리된 데이터를 다른 곳에 저장 sum_hf_yr_OBP_origin = sum_hf_yr_OBP.copy() # 전체 희생타 계산 regular_season_df['SF'] = \ regular_season_df[['H','BB','HBP']].sum(axis=1) / regular_season_df['OBP'] - \ regular_season_df[['AB','BB','HBP']].sum(axis=1) regular_season_df['SF'].fillna(0, inplace = True) regular_season_df['SF'] = regular_season_df['SF'].apply(lambda x : round(x,0)) # 한 타수당 평균 희생타 계산 후 필요한 것만 추출 regular_season_df['SF_1'] = regular_season_df['SF'] / regular_season_df['AB'] regular_season_df_SF = regular_season_df[['batter_name','year','SF_1']] #day_by_day에서 연도별 선수의 시즌 전반기 출루율과 관련된 성적 합 구하기 + BB, RBI 추가 sum_hf_yr_OBP = \ day_by_day_df.loc[day_by_day_df['date'] <= 7.18].groupby(['batter_name','year'])[ 'AB','H','BB','HBP','RBI', '2B', '3B', 'HR'].sum().reset_index() #day_by_day와 regular season에서 구한 희생타 관련 데이터를 합치기 sum_hf_yr_OBP = sum_hf_yr_OBP.merge(regular_season_df_SF, how = 'left', on=['batter_name','year']) # 한 타수당 평균 희생타 계산 sum_hf_yr_OBP['SF'] = \ (sum_hf_yr_OBP['SF_1']*sum_hf_yr_OBP['AB']).apply(lambda x: round(x,0)) sum_hf_yr_OBP.drop('SF_1',axis = 1, inplace = True) # 전반기 OBP(출루율 계산) sum_hf_yr_OBP['OBP'] = sum_hf_yr_OBP[['H', 'BB', 'HBP']].sum(axis = 1) / \ sum_hf_yr_OBP[['AB', 'BB', 'HBP','SF']].sum(axis = 1) sum_hf_yr_OBP['OBP'].fillna(0, inplace = True) # TB 계산 sum_hf_yr_OBP['TB'] = sum_hf_yr_OBP['H'] + sum_hf_yr_OBP['2B']*2 + \ sum_hf_yr_OBP['3B']*3 + sum_hf_yr_OBP['HR']*4 sum_hf_yr_OBP = sum_hf_yr_OBP[['batter_name','year','AB','OBP', 'BB', 'TB', 'RBI']] # 나이 추가 sum_hf_yr_OBP = sum_hf_yr_OBP.merge(regular_season_df[['batter_name','year','age']], how = 'left', on=['batter_name','year']) # 평균 OBP 추가 sum_hf_yr_OBP = sum_hf_yr_OBP.merge(player_OBP_mean[['batter_name', 'mean_OBP']], how ='left', on="batter_name") sum_hf_yr_OBP = \ sum_hf_yr_OBP.loc[~sum_hf_yr_OBP['mean_OBP'].isna()].reset_index(drop=True) -
OBP만 이용했을 때 모델링에 사용하는 변수를
feature_list_1에 저장하고 볼넷(BB). 루타 (TB), 타점(BRI)을 추가해 모델링할 때 사용하는 변수를feature_list_2에 저장 -
단순 비교를 위해 결측치는 따로 처리하지 않을 것이며 결측치가 포함된 데이터는 제거하고 모델링 작업을 진행
-
모델링에 사용하는 변수 리스트 지정
# 각 변수에 대한 1년 전 성적 생성 sum_hf_yr_OBP = lag_function(sum_hf_yr_OBP, "BB", 1) sum_hf_yr_OBP = lag_function(sum_hf_yr_OBP, "TB", 1) sum_hf_yr_OBP = lag_function(sum_hf_yr_OBP, "RBI", 1) sum_hf_yr_OBP = lag_function(sum_hf_yr_OBP, "OBP", 1) sum_hf_yr_OBP = sum_hf_yr_OBP.dropna() # 결측치 포함한 행 제거 # 변수 리스트 지정 feature_list_1 = ['age', 'lag1_OBP', 'mean_OBP'] feature_list_2 = ['age', 'lag1_BB', 'lag1_TB', 'lag1_RBI','lag1_OBP', 'mean_OBP'] -
OBP_RF_models_1은age와mean_OBP, 1년 전 OBP 값을 이용해 학습한 모델 -
OBP_RF_ models_2는OBP_RF_models_1에서 사용한 변수에 OBP와 높은 상관관계를 보였던 1년 전 RBI, TB. BB 값을 변수로 추가해 학습한 모델 -
두 모델 다 GridSearchCV를 통해 최적 의 모수를 설정함
-
학습
# 학습시킬 데이터 30타수 이상만 학습 sum_hf_yr_OBP= sum_hf_yr_OBP.loc[sum_hf_yr_OBP['AB']>=30] # 2018년 test로 나누고 나머지는 학습 OBP_train = sum_hf_yr_OBP.loc[sum_hf_yr_OBP['year'] != 2018] OBP_test = sum_hf_yr_OBP.loc[sum_hf_yr_OBP['year'] == 2018] # grid search를 이용해 학습한다. OBP_RF_models_1 = { 'RF': GridSearchCV( RandomForestRegressor(random_state=42), param_grid=RF_params, n_jobs=-1 ).fit(OBP_train.loc[:,feature_list_1], OBP_train['OBP']).best_estimator_} OBP_RF_models_2 = { 'RF': GridSearchCV( RandomForestRegressor(random_state=42), param_grid=RF_params, n_jobs=-1 ).fit(OBP_train.loc[:,feature_list_2], OBP_train['OBP']).best_estimator_} -
결과를 비교했을 때 두 모델 간 WRMSE 값의 차이가 0.002로 매우 미세함
-
두 모델이 비슷한 성능을 보이고 있다면 분석을 진행할 때 가능한 변수가 적은 모델을 선택해야 함
-
실제 2019년 상반기 데이터를 대상으로 예측을 진행할 때 변수가 많을수록 과적합 이슈가 발생할 수 있기 때문
-
정밀하게 예측을 하려면 최대한 단순화된 모델을 생성하는 것이 필요
-
필요하다면 SLG나 다른 변수를 추가해 다양한 실험을 해볼 수 있음
-
두 모델의 WRMSE 비교
# 예측 RF_OBP_1 = OBP_RF_models_1['RF'].predict(OBP_test.loc[:,feature_list_1]) RF_OBP_2 = OBP_RF_models_2['RF'].predict(OBP_test.loc[:,feature_list_2]) # wrmse 계산 wrmse_score = [wrmse(OBP_test['OBP'],OBP_test['AB'],RF_OBP_1) , wrmse(OBP_test['OBP'],OBP_test['AB'],RF_OBP_2)] x_lab = ['simple', 'complicate'] plt.bar(x_lab, wrmse_score) plt.title('WRMSE of OBP', fontsize=20) plt.xlabel('model', fontsize=18) plt.ylabel('', fontsize=18) plt.ylim(0,0.5) # 막대그래프 위에 값을 표시해준다. for i, v in enumerate(wrmse_score): plt.text(i-0.1, v + 0.01, str(np.round(v,3))) # x 좌표, y좌표, 텍스트 표시 plt.show()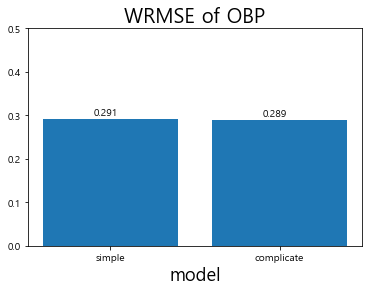
-
최종 제출을 위한 원래 데이터 복구
# 최종 제출을 위한 원래 데이터 복구 sum_hf_yr_OBP = sum_hf_yr_OBP_origin.copy()
5_3 테스트 데이터 정제
-
지금까지는 학습의 성능을 평가하기 위해 실제 대회의 예측 대상인 2019 시즌이 아닌 2018 시즌의 데이터를 기준으로 모델링을 진행
-
지금부터는 실제로 이 대회에 결과물을 제출하기 위한 2019 시즌 대상의 모델링 작업을 진행
-
주어진 submission.csv 파일에 2019년 성적을 예측할 선수 명단이 있으므로 이 파일을 불러와 해당 선수에 대해 학습 데이터와 같이 전처리를 진행
-
그리고 동일한 submission 파일을 2개로 복사해 하나는 OBP, 다른 하나는 SLG 성적을 예측하고 두 개의 예측 값을 더해 최종 OPS를 예측하는 방식을 이용
-
2019년 데이터 전처리
submission = pd.read_csv('C:/dacon/ch01/dataset/submission.csv') submission['year'] = 2019 # 연도 기입 # 2019년의 Age(나이) 계산 batter_year_born = regular_season_df[['batter_id','batter_name','year_born']].copy() # 중복선수 제거 batter_year_born = batter_year_born.drop_duplicates().reset_index(drop=True) submission = submission.merge(batter_year_born, how='left', on=['batter_id', 'batter_name']) submission['age'] = submission['year'] - \ submission['year_born'].apply(lambda x: int(x[:4])) submission.head()batter_id batter_name year year_born age 0 1 강경학 2019 1992년 08월 11일 27 1 2 강구성 2019 1993년 06월 09일 26 2 3 강민국 2019 1992년 01월 10일 27 3 4 강민호 2019 1985년 08월 18일 34 4 5 강백호 2019 1999년 07월 29일 20 -
주어진 파일을 읽어온 후 나이 변수 생성
-
이제 이 데이터를 두 개로 복사해 출루율과 장타율 각각에 대한 데이터 처리 작업을 진행
-
출루율부터 선수별로 과거 성적 및 평균 성적 변수를 만들어 추가
-
데이터를 복사
# submission OBP, SLG 파일 2개 만들어 합치기 submission_OBP = submission.copy() submission_SLG = submission.copy()
OBP
-
앞서 전처리한
sum_hf_yr_0BP를 이용 -
OPS 예측 결과를 제출해야 할 선수들의 평균 성적을 불러오고 과거의 성적을 생성
-
과거 출루율을 생성
# 앞서 전처리한 데이터를 이용해 평균 성적 기입 submission_OBP = submission_OBP.merge( sum_hf_yr_OBP[['batter_name','mean_OBP']].drop_duplicates().reset_index(drop=True), how = 'left', on ='batter_name') # 앞서 전처리한 데이터를 이용해 과거 성적 값 채우기 for i in [1,2,3]: temp_lag_df = sum_hf_yr_OBP.loc[ (sum_hf_yr_OBP['year'] == (2019 - i)) & (sum_hf_yr_OBP['AB']>=30),['batter_name','OBP']].copy() temp_lag_df.rename(columns={'OBP':'lag'+str(i)+'_OBP'}, inplace=True) submission_OBP = submission_OBP.merge(temp_lag_df, how='left', on='batter_name') submission_OBP.head()batter_id batter_name year year_born age mean_OBP lag1_OBP lag2_OBP lag3_OBP 0 1 강경학 2019 1992년 08월 11일 27 0.337880 0.423611 0.285714 0.222222 1 2 강구성 2019 1993년 06월 09일 26 NaN NaN NaN NaN 2 3 강민국 2019 1992년 01월 10일 27 NaN NaN NaN NaN 3 4 강민호 2019 1985년 08월 18일 34 0.358187 0.328990 0.386076 0.441860 4 5 강백호 2019 1999년 07월 29일 20 0.356164 0.355685 NaN NaN -
처리를 하다보니 결즉치가 발생
-
앞에서는 결즉치를 삭제하고 모델링
-
하지만 지금은 결측치 삭제 방식을 이용하지 못함
-
결측치를 삭제하면 대회에 제출해야 할 선수의 데이터 자체가 사라지기 때문
-
결측치를 어떻게 처리하면 좋을지 판단하기 위해 평균 성적이 결측치인 선수들을 봄.
-
출루율에 결측치가 있는 선수
submission_OBP['batter_name'].loc[submission_OBP['mean_OBP'].isna()].valuesarray(['강구성', '강민국', '강상원', '고명성', '김응민', '김종덕', '김주찬', '김철호', '김태연', '김태진', '김형준', '나원탁', '남태혁', '박광열', '박기혁', '백민기', '샌즈', '신범수', '신성현', '양종민', '윤정우', '이동훈', '이범호', '이병휘', '이성곤', '이인행', '이종욱', '이진영', '이창진', '장승현', '장시윤', '전민재', '전병우', '정경운', '정성훈', '조홍석', '최원제', '홍창기'], dtype=object) -
위와 같이 평균 성적이 결측치인 선수의 명단을 만듦
-
해당 선수들은 총 4가지의 케이스로 분류해 결측치 처리를 하겠습니다.
-
case 1
-
첫 번째 케이스는 정규시즌 데이터(regular_season_Batter)에는 있으나 일별 데이터 (Regular_Season_Batter_Day)에는 기록이 없어 결측치가 생긴 선수
-
이 사례에 해당하는 선수는 김주찬, 이범호
-
이 경우는 정규시즌 데이터를 이용해 결측치를 처리
-
또한 다행히 첫 번째 케이스는 정규시즌 데이터를 통해 1, 2, 3년 전의 성적 역시 구할 수 있음.
일별 데이터 출루율 결측치 처리
for batter_name in ["김주찬", "이범호"]: # 30타수 이상인 해당선수의 인덱스(Boolean) cond_regular = (regular_season_df['AB'] >= 30) & \ (regular_season_df['batter_name'] == batter_name) # 타수를 고려해 평균 OBP 계산 mean_OBP = sum(regular_season_df.loc[cond_regular,'AB'] * \ regular_season_df.loc[cond_regular,'OBP']) / \ sum(regular_season_df.loc[cond_regular,'AB']) submission_OBP.loc[(submission_OBP['batter_name'] == batter_name),'mean_OBP'] = \ mean_OBP # regular_season_Batter으로부터 1, 2, 3년 전 성적 구하기 cond_sub = submission_OBP['batter_name'] == batter_name submission_OBP.loc[cond_sub,'lag1_OBP'] = regular_season_df.loc[ (cond_regular) & (regular_season_df['year']==2018),'OBP'].values submission_OBP.loc[cond_sub,'lag2_OBP'] = regular_season_df.loc[ (cond_regular) & (regular_season_df['year']==2017),'OBP'].values submission_OBP.loc[cond_sub,'lag3_OBP'] = regular_season_df.loc[ (cond_regular) & (regular_season_df['year']==2016),'OBP'].values
-
-
case2
-
두 번째 케이스는 1998년 혹은 1999년 출생의 신인급 선수
-
이 사례에 해당하는 선 수는 고명성, 전민재, 김철호, 신범수, 이병휘
-
앞서 나이에 따른 OPS성적 변화를 살펴봤을 때 나이가 어린 경우 이후 성적이 더 높아지는 경향이 있음
-
두 번째 케이스에 해당하는 선수들은 성장 가능성이 있어 평균 이상을 기대할 수 있는 선수로 판단하고 2018 시즌의 성적으로 출루율의 평균을 대체
신인 선수의 출루율 결측치 처리
for i in np.where(submission_OBP['batter_name'].isin(["고명성","전민재","김철호","신범수","이병휘"])): #submission_OBP.loc[i,'mean_OBP'] = season_OBP_mean.loc[season_OBP_mean['year']==2018,'mean_OBP'].values submission_OBP.loc[i,'mean_OBP'] = \ season_OBP_mean.loc[season_OBP_mean['year']==2018,'mean_OBP']
-
-
case3
-
세 번째 케이스는 2018년 하반기의 성적만 있는 경우
-
이에 해당하는 선수는 샌즈, 전병우
-
해당 선수들은 정규시즌 성적을 바탕으로 평균 출루율 및 1년 전 출루율 수치를 대체
상반기 출루율 결측치 처리
for batter_name in ["전병우","샌즈"]: # 30 타수 이상인 해당 선수의 index 추출 cond_regular = (regular_season_df['AB']>=30) & \ (regular_season_df['batter_name']==batter_name) # 타수를 고려해 선수의 평균 OBP계산 mean_OBP = sum(regular_season_df.loc[cond_regular,'AB'] * \ regular_season_df.loc[cond_regular,'OBP']) / \ sum(regular_season_df.loc[cond_regular,'AB']) submission_OBP.loc[(submission_OBP['batter_name'] == batter_name),'mean_OBP'] = mean_OBP cond_sub = submission_OBP['batter_name'] == batter_name # 2018년 데이터로부터 2019년의 1년 전 성적 기입 submission_OBP.loc[cond_sub,'lag1_OBP'] = regular_season_df.loc[ (cond_regular)&(regular_season_df['year']==2018),'OBP'].values
-
-
case4
-
마지막 케이스는 은퇴를 했거나 1군 수준의 성적을 보여주지 못하는 선수
-
이 선수 들의 성적은 하위 25%의 성적으로 대체해서 값을 넣음
평균 출루율 결측치 처리
# 평균 성적이 결측치인 선수들에 대해 평균 OBP의 하위 25% 성적 기입 submission_OBP.loc[submission_OBP['mean_OBP'].isna(),'mean_OBP'] = \ np.quantile(player_OBP_mean['mean_OBP'],0.25)
-
-
지금까지 평균 출루율 성적에 대해 모두 결측치 처리를 완료함
-
이제 앞서 생성한 결측 치 처리 함수인
lag_na_fill을 이용해 평균 성적이 아닌 1, 2, 3년 전 성적의 결측치 처리를 진행3년 전까지의 평균 출루율 결측치 처리
for i in [1,2,3]: # i년 전 OBP 결측치 제거 submission_OBP = lag_na_fill(submission_OBP, 'OBP', i, season_OBP_mean) submission_OBP.head()batter_id batter_name year year_born age mean_OBP lag1_OBP lag2_OBP lag3_OBP 0 1 강경학 2019 1992년 08월 11일 27 0.337880 0.423611 0.285714 0.222222 1 2 강구성 2019 1993년 06월 09일 26 0.304124 0.329991 0.330297 0.336224 2 3 강민국 2019 1992년 01월 10일 27 0.304124 0.329991 0.330297 0.336224 3 4 강민호 2019 1985년 08월 18일 34 0.358187 0.328990 0.386076 0.441860 4 5 강백호 2019 1999년 07월 29일 20 0.356164 0.355685 0.356317 0.362245
SLG
-
과거 장타율을 생성
# 앞서 전처리한 데이터로 평균 SLG 값 기입 submission_SLG = submission_SLG.merge( sum_hf_yr_SLG[['batter_name','mean_SLG']].drop_duplicates().reset_index(drop=True), how='left', on='batter_name') # 앞서 전처리한 데이터에서 과거 SLG 값 채우기 for i in [1,2,3]: temp_lag_df = sum_hf_yr_SLG.loc[(sum_hf_yr_SLG['year'] == (2019 - i)) & (sum_hf_yr_SLG['AB']>=30),['batter_name','SLG']].copy() temp_lag_df.rename(columns={'SLG':'lag'+str(i)+'_SLG'}, inplace=True) submission_SLG = submission_SLG.merge(temp_lag_df, how='left', on='batter_name') -
결측치 존개 선수 명단 확인
장타율에 결측치가 있는 선수
submission_SLG['batter_name'].loc[submission_SLG['mean_SLG'].isna()].valuesarray(['강구성', '강민국', '강상원', '고명성', '김응민', '김종덕', '김주찬', '김철호', '김태연', '김태진', '김형준', '나원탁', '남태혁', '박광열', '박기혁', '백민기', '샌즈', '신범수', '신성현', '양종민', '윤정우', '이동훈', '이범호', '이병휘', '이성곤', '이인행', '이종욱', '이진영', '이창진', '장승현', '장시윤', '전민재', '전병우', '정경운', '정성훈', '조홍석', '최원제', '홍창기'], dtype=object) -
장타율에 결즉치가 있는 선수 명단은 출루율에 결측치가 있는 선수 명단과 동일한 것을 확인 가능
-
출루율과 마찬가지로 4가지 케이스로 분류해 결측치 처리를 진행
-
case1
-
첫 번째 케이스인 정규시즌 데이터에는 기록이 있지만 일별 데이터에는 기록이 없는 선수들 에 대한 장타율 결측치 처리
일별 데이터 장타율 결측치 처리
for batter_name in ["김주찬", "이범호"]: # mean_SLG 계산 cond_regular = (regular_season_df['AB'] >= 30) & \ (regular_season_df['batter_name'] == batter_name) # 타수를 고려해 선수의 평균 SLG 계산 mean_SLG = sum(regular_season_df.loc[cond_regular,'AB'] * \ regular_season_df.loc[cond_regular,'SLG']) / \ sum(regular_season_df.loc[cond_regular,'AB']) submission_SLG.loc[(submission_SLG['batter_name'] == batter_name), 'mean_SLG'] = \ mean_SLG # regular_season_Batter으로부터 1, 2, 3년 전 성적 구하기 cond_sub = submission_SLG['batter_name'] == batter_name submission_SLG.loc[cond_sub,'lag1_SLG'] = regular_season_df.loc[ (cond_regular) & (regular_season_df['year'] == 2018),'SLG'].values submission_SLG.loc[cond_sub,'lag2_SLG'] = regular_season_df.loc[ (cond_regular) & (regular_season_df['year'] == 2017),'SLG'].values submission_SLG.loc[cond_sub,'lag3_SLG'] = regular_season_df.loc[ (cond_regular) & (regular_season_df['year'] == 2016),'SLG'].values
-
-
case2
-
두 번째 케이스인 1998년 혹은 1999년 출생인 신인 선수들에 대한 장타율 결측치 처리
신인 선수의 장타율 결측치 처리
for i in np.where(submission_SLG['batter_name'].isin( ["고명성","전민재","김철호","신범수","이병휘"])): # 위의 해당 선수들의 평균 SLG 평균값으로 대체 #submission_SLG.loc[i,'mean_SLG'] = season_SLG_mean.loc[season_SLG_mean['year']==2018,'mean_SLG'].values submission_SLG.loc[i,'mean_SLG'] = \ season_SLG_mean.loc[season_SLG_mean['year']==2018,'mean_SLG']
-
-
case3
-
세 번째 케이스인 상반기 기간의 데이터가 존재하지 않는 선수들에 대한 장타율 결측치 처리
상반기 장타율 결측치 처리
for batter_name in ["전병우","샌즈"]: # 30타수 이상인 해당선수의 인덱스(Boolean) cond_regular = (regular_season_df['AB']>=30)&\ (regular_season_df['batter_name']==batter_name) # 타수를 고려한 평균 SLG 계산 mean_SLG = sum(regular_season_df.loc[cond_regular,'AB']* regular_season_df.loc[cond_regular,'SLG']) / sum(regular_season_df.loc[cond_regular,'AB']) # 해당 선수의 평균 SLG 값 기입 submission_SLG.loc[(submission_SLG['batter_name'] == batter_name), 'mean_SLG'] = mean_SLG # 해당 선수의 1년 전 SLG값 기입 cond_sub = submission_SLG['batter_name'] == batter_name submission_SLG.loc[cond_sub,'lag1_SLG'] = regular_season_df.loc[(cond_regular)& (regular_season_df['year']==2018),'SLG'].values
-
-
case4
-
네 번째 케이스는 은퇴를 했거나 1군 수준의 성적을 보여주지 못하는 선수들 대한 장타율 결측치 처리
평균 장타율 결측치 처리
# 평균 성적이 결측치인 선수들에 대해 평균 SLG의 하위 25% 성적 기입 submission_SLG.loc[submission_SLG['mean_SLG'].isna(),'mean_SLG'] = \ np.quantile(player_SLG_mean['mean_SLG'],0.25)
-
-
테스트용 데이터에 대해서도 평균 장타율에 대한 결측치 처리를 완료
-
출루율과 마찬가지로 평균 장타율을 기반으로 1, 2, 3년 전 장타율을 추가
3년 전까지의 평균 장타율 결측치 처리
for i in [1,2,3]: # i년 전 SLG 성적 결측치 처리 submission_SLG = lag_na_fill(submission_SLG, 'SLG', i, season_SLG_mean) submission_SLG.head()batter_id batter_name year year_born age mean_SLG lag1_SLG lag2_SLG lag3_SLG 0 1 강경학 2019 1992년 08월 11일 27 0.332527 0.523810 0.256098 0.222222 1 2 강구성 2019 1993년 06월 09일 26 0.326923 0.391429 0.385754 0.385397 2 3 강민국 2019 1992년 01월 10일 27 0.326923 0.391429 0.385754 0.385397 3 4 강민호 2019 1985년 08월 18일 34 0.466540 0.487273 0.548736 0.577689 4 5 강백호 2019 1999년 07월 29일 20 0.523719 0.532051 0.484152 0.483795 -
이제 테스트용 데이터에 대해서도 전처리 및 변수 생성 작업이 완료됨
-
지금부터 최종 2019년 KBO 상반기 타자 OPS 예측 결과를 도출
-
알고리즘별 성능 비교에서 OBP를 예측할 때는 랜덤 포레스트가 가장 우수한 성능을 보였고 SLG를 예측할 때는 라쏘 회귀 모델이 가장 우수한 성능을 보임
-
따라서 OBP와 SLG 에서 우수한 성능을 보인 알고리즘을 이용해 예측값을 생성
OBP와 SLG 예측값 생성
# Random Forests를 이용해 OBP 예측 predict_OBP = OBP_RF_models['RF'].predict(submission_OBP.iloc[:,-5:]) # Lasso를 이용해 SLG 예측 predict_SLG = SLG_linear_models ['Lasso'].predict(submission_SLG.iloc[:,-5:]) -
경진대회 양식에 맞는 최종 파일을 제출하기 위해 submission 데이터셋에서
batter_id와batter_name을 가져와 final_submission에 저장 -
예측된 OBP와 SLG 값을 더해 타 자의 2019년 0PS를 예측
-
이로써 최종 제출을 위한 데이터셋이 완성
OPS 예측
final_submission = submission[['batter_id','batter_name']] final_submission['OPS'] = predict_SLG + predict_OBP # OBP + SLG = OPS final_submission.head(10)C:\Users\kimminsung\AppData\Roaming\Python\Python36\site-packages\ipykernel_launcher.py:2: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
batter_id batter_name OPS 0 1 강경학 0.503957 1 2 강구성 0.687933 2 3 강민국 0.696609 3 4 강민호 0.958395 4 5 강백호 0.751592 5 8 강상원 0.661807 6 9 강승호 0.505642 7 11 강진성 0.656007 8 12 강한울 0.672859 9 16 고명성 0.640507
5_4 반발계수의 변화
-
앞서 대회를 위한 최종 제출 파일을 완성
- 이제 마지막으로 2019년의 특징성을 반영해 최종 모델링을 완료
- 2019년이라는 시즌의 특징을 살펴보면 2019년 상반기 KBO 타자의 성적을 더 정확히 예측 가능
- 그러한 면에서 생각했을 때, 2019 시즌에 타자들에게 가장 큰 영향을 줄 수 있는 변화는 바로 공인구의 반발계수 변화
- 반발계수란 물체가 충돌했을 때 충돌 전후 속도의 비를 의미
- 야구에서 공인구의 반발계수가 달라진다면 야구 배트와 야구공의 충돌 전후 야구공 속도의 비가 달라짐
- 충돌 후의 속도가 전과 달라진다면 야구공이 날아가는 거리에도 영향을 미침
- 2019 시즌에 KBO는 새롭게 반발계수를 낮춘 야구공을 이용
-
공인구의 반발계수 변화는 타자들의 성적에 유의미하게 영향을 줌
- 반발계수를 낮춘 야구공을 사용한다는 것은 전과 동일한 힘으로 공을 쳤을 때 공이 이전 공(반발계수 를 낮추기 전의 공)보다 더 조금 날아간다는 것을 의미하기 때문
- 선수의 역량이 같더라도 어느 정도의 성적 하락 현상이 발생 가능
- 이를 타당하게 반영하기 위해 과거 일본 사례를 참고
- 공인구 반발계수를 똑같이 조정한 적이 있는 일본 사례에서는 홈런이 이전 시즌보다 약 절반으로 줄어듦
- 홈런 개수라는 반발계수 변화 효과에 대한 단서가 생겼으므로 이를 바탕으로 공인구 변화의 효과를 예측
홈런 수 병합
# 시즌별 전체 OBP 계산(30타수 이상인 선수들의 기록만 이용) season_OBP = \ regular_season_df.loc[regular_season_df['AB'] >= 30].groupby('year').agg( {'AB':'sum', 'H':'sum', 'BB':'sum', 'HBP':'sum', 'SF':'sum'}).reset_index() season_OBP['OBP'] = season_OBP[['H','BB','HBP']].sum(axis=1) / \ season_OBP[['AB','BB','HBP','SF']].sum(axis=1) # 시즌별 전체 SLG 계산(30타수 이상인 선수들의 기록만 이용) season_SLG = \ regular_season_df.loc[regular_season_df['AB']>=30].groupby('year').agg( {'AB':'sum', 'H':'sum', '2B':'sum', '3B':'sum', 'HR':'sum'}).reset_index() season_SLG['SLG'] = ((season_SLG['H'] - season_SLG[['2B','3B','HR']].sum(axis=1)) + \ season_SLG['2B']*2+season_SLG['3B']*3+ season_SLG['HR']*4) / \ season_SLG['AB'] # season_OBP와 season_SLG를 병합 후 season_OPS를 생성해 OPS 계산 season_OPS = pd.merge(season_OBP[['year','OBP']],season_SLG[['year', 'SLG']], on = 'year') season_OPS['OPS'] = season_OPS['OBP'] + season_OPS['SLG'] # 시즌별 전체 홈런 수와 한 선수당 평균 홈런 수 계산 season_HR = regular_season_df.loc[regular_season_df['AB']>=30].groupby('year').agg( {'HR':['sum','mean','count']}).reset_index() season_HR.columns = ['year', 'sum_HR', 'mean_HR', 'count'] # 기존의 OPS 데이터셋과 병합 season_OPS = season_OPS.merge(season_HR,on ='year' ,how='left') display(season_OPS.tail())year OBP SLG OPS sum_HR mean_HR count 21 2014 0.368970 0.446302 0.815272 1013 7.235714 140 22 2015 0.362742 0.434129 0.796871 1222 7.685535 159 23 2016 0.368325 0.443871 0.812196 1267 7.918750 160 24 2017 0.356469 0.444584 0.801053 1450 8.285714 175 25 2018 0.355858 0.455936 0.811794 1726 9.806818 176 -
2018 시즌에 30타수 이상을 기록한 선수의 홈런은 총 1,726개
-
1.762/2=863이므로 863개의 홈런이 줄어들었을 때 OPS가 얼마나 감소하는지를 봄
-
다만, 홈런이 될 타구가 홈런이 되지 않더라도 안타가 되어 OPS 하락에는 영향을 미치지 않을 가능 성도 있음.
-
따라서 안타와 아웃 두 가지의 경우로 나누어 863/2=431.5라는 홈런 개수가 실제 OPS 하락에 영향을 미친다고 가정
-
431.5개의 홈런 개수를 2018시즌 30타수 이상을 기록한 타자의 수로 나누면 431.5/176= 2.45입니다. 즉 홈런 개수가 평균적으로 2.45개 적은 시즌의 OPS 수치를 참고할 수 있음
2018년 평균 홈런 개수와 시즌별 평균 홈런 수의 차이
#2018년의 평균 홈런 개수를 시즌별 평균 홈런 수에서 뺀다(HR_diff) season_OPS['HR_diff'] = season_OPS['mean_HR'] - season_OPS['mean_HR'].iloc[-1] difference = season_OPS.sort_values(by = 'HR_diff')[['year','OPS','HR_diff']] display(difference.reset_index(drop=True).head(12))year OPS HR_diff 0 2012 0.703301 -5.799242 1 2013 0.748820 -4.891325 2 2006 0.709301 -4.806818 3 2008 0.741542 -4.671987 4 2011 0.735087 -4.564883 5 2007 0.730715 -4.451555 6 2005 0.740615 -3.543660 7 2010 0.770265 -2.623332 8 2014 0.815272 -2.571104 9 2004 0.751737 -2.500696 10 2001 0.821178 -2.152972 11 2015 0.796871 -2.121284 -
2018 시즌과의 홈런 개수 차이를 의미하는
HR_diff값이 -2.45와 가장 근접한 연도는 2004년으로 -2.50이며 2014년이 -2.57로 두 번째, 2010년이 -2.62로 세 번째로 근접 -
2004년의 데이터부터 자세히 봄
2000년까지의 데이터 제외
# 2000년도 이전의 데이터 수가 충분치 않아 고려하지 않는다. season_OPS.loc[season_OPS['year']>2000]year OBP SLG OPS sum_HR mean_HR count HR_diff 8 2001 0.366585 0.454593 0.821178 199 7.653846 26 -2.152972 9 2002 0.343798 0.424739 0.768536 274 8.838710 31 -0.968109 10 2003 0.353936 0.427291 0.781227 301 7.717949 39 -2.088869 11 2004 0.344181 0.407556 0.751737 358 7.306122 49 -2.500696 12 2005 0.344851 0.395764 0.740615 357 6.263158 57 -3.543660 13 2006 0.334390 0.374912 0.709301 345 5.000000 69 -4.806818 14 2007 0.346222 0.384493 0.730715 407 5.355263 76 -4.451555 15 2008 0.350637 0.390905 0.741542 457 5.134831 89 -4.671987 16 2009 0.359326 0.429237 0.788563 806 8.141414 99 -1.665404 17 2010 0.356988 0.413278 0.770265 783 7.183486 109 -2.623332 18 2011 0.348382 0.386705 0.735087 650 5.241935 124 -4.564883 19 2012 0.337141 0.366160 0.703301 529 4.007576 132 -5.799242 20 2013 0.355484 0.393335 0.748820 698 4.915493 142 -4.891325 21 2014 0.368970 0.446302 0.815272 1013 7.235714 140 -2.571104 22 2015 0.362742 0.434129 0.796871 1222 7.685535 159 -2.121284 23 2016 0.368325 0.443871 0.812196 1267 7.918750 160 -1.888068 24 2017 0.356469 0.444584 0.801053 1450 8.285714 175 -1.521104 25 2018 0.355858 0.455936 0.811794 1726 9.806818 176 0.000000 -
2004년에는 30타수 이상을 기록한 타자 수가 49명
- 주어진 데이터의 30타수 이상 기록 타자 수가 2010년부터 100명 이상으로 안정화되고 있어 2004년 데이터는 제외
-
2014년에는 홈런 차이는 근접하지만, OPS가 전체 시즌 중 가장 높은 수치를 기록
- 오히려 2018년보다 더 높은 OPS를 보여주고 있어 홈런 감소가 OPS 하락에 미치는 영 향을 판단하기에는 부적절
-
2010년의 데이터는 2018년보다 OPS가 낮으며 타자 수도 100명 이상을 기록
- 두 연도를 비교해 본 결과 OPS는 평균적으로 0.041(2018년의 OPS = 0.81, 2010년의 OPS = 0.77), 홈런 개수는 평균적으로 2.62개의 차이를 보임
- 예상되는 2018 시즌 대비 2019 시즌 평균 홈런 개수 차이는 2.45이므로 이 비중을 조금 더 정밀하게 계산
-
2.45x0.041/2.62=0.038로 홈런 개수의 감소로 인해 약 0.038의 OPS 하락이 있을 것으로 예측 가능
-
이제 예측된 2019 시즌 상반기 KBO 타자 OPS 성적에서 일괄적으로 0.038 수치를 빼 새로운 예측 결과물을 생성
2019년 공인구 반발계수 변화를 반영
final_submission['OPS'] = final_submission['OPS'] - 0.038 display(final_submission.head(10)) final_submission.to_csv('submission.csv', index=False) # 최종 제출파일 생성C:\Users\kimminsung\AppData\Roaming\Python\Python36\site-packages\ipykernel_launcher.py:1: SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame. Try using .loc[row_indexer,col_indexer] = value instead See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy """Entry point for launching an IPython kernel.batter_id batter_name OPS 0 1 강경학 0.465957 1 2 강구성 0.649933 2 3 강민국 0.658609 3 4 강민호 0.920395 4 5 강백호 0.713592 5 8 강상원 0.623807 6 9 강승호 0.467642 7 11 강진성 0.618007 8 12 강한울 0.634859 9 16 고명성 0.602507 -
2019년 공인구 반발계수 변화까지 반영해 최종 예측값을 도출
-
최종 예측 결과물은
final_submission이라는 이름의 데이터프레임에 저장 -
final_submission을 submission.csv로 저장해 데이콘에 제출
6_ 정리📑
- 지금까지 경진대회 개요 파악, 탐색적 데이터 분석, 데이터 전처리, 모델 구축과 검증, 성능 향상을 위한 기법을 적용해 최종 예측 결과물을 만듦
- 경진대회 개요를 통해 요구사 항 파악하기를 시작으로 탐색적 데이터 분석을 통한 전체 분석 전략 수립, 데이터 전처리를 통한 필요 데이터 정제, 모델링을 통한 머신러닝 수행, 성능 향상 기법을 통한모델 성능 고도화까지의 작업을 진행
- 이러한 절차는 이번 대회뿐만 아니라 다양한 데이터 분석 대 회에 모두 적용 가능
- 단계별로 이번 예제에서 파악하지 못했던 새로운 정보를 발견하거나 분석 전략에 있어 창의 적인 아이디어를 개발한다면 예제보다 더 성능 좋은 모델을 개발할 수 있을 것으로 기대
- 자신만 의 분석 논리를 만들어 이를 실제로 구현한 후 그 결과를 본 예제와 비교해본다면 더 유익하 게 데이터 분석 역량을 쌓을수 있음
댓글남기기