⚾Chapter01 KBO 타자 OPS 예측 2 - 데이터 전처리, 모델 구축과 검증

• ⚾Chapter01 KBO 타자 OPS 예측 1 - 문제 정의, 탐색적 데이터 분석
• ⚾Chapter01 KBO 타자 OPS 예측 3 - 성능 향상을 위한 방법, 정리

3_ 데이터 전처리📑

• 데이터 전처리 : 분석과 예측 모델링 작업을 진행할 수 있게 데이터를 정제하고 변환하는 모든 작업을 의미함.
  • 데이터가 비어 있는 결측치의 처리
  • 잘못된 데이터 라고 판단되는 데이터의 오류 처리
  • 규정 타수 정의
  • 시간 변수를 포함한 추가 변수 생성
  • 최종 데이터 정제

3_1 결측치 처리 및 데이터 오류 처리

• 데이터 수집 과정이나 환경 문제로 인해 결측치나 오류 발생 가능

• 결측치 문제를 먼저 해결하기 위해 다음의 데이터에 대해 결측치 처리를 먼저 수행

  • 정규시즌 데이터와 일별 데이터
  • 프리시즌 데이터

• 결측치 개수 확인

  pd.DataFrame(regular_season_df.isna().sum()).transpose()
    
  # 실행결과
  	batter_id	batter_name	year	team	avg	G	AB	R	H	2B	...	position	career	starting_salary	OPS	weight	height	weight_per_height	pos	hit_way	country
  0	0	0	0	0	26	0	0	0	0	0	...	802	0	1076	26	802	802	802	802	802	0
  1 rows × 35 columns
  

• 확인 결과 타율(avg), 장타율(SLG), 출루율(OBP) 등의 변수에 결측치가 존재

• 데이터 타입에 따라 결측치 처리 방법이 달라질 수 있으므로 수치형 타입의 변수만 따로 추출해 결측치를 처리

• 수치형 타입 변수의 결측치 현황을 확인하기 위해 결측치가 존재하는 행을 출력

• 연도별 평균 타율

  # 수치형 타입의 변수 저장
  numerics = [
      'int16', 'int32', 'int64', 'float16', 'float32', 'float64'] # 모든 numeric(수치형) 타입
  num_cols = regular_season_df.select_dtypes(include=numerics).columns
    
  # 수치형 타입 변수 중 결측치가 하나라도 존재하는 행 출력
  # isna().sum(axis=1) -> 열 기준의 결측치 개수
  # df.loc[]를 통해 결측치 0개 이상 데이터를 추출
  regular_season_df.loc[regular_season_df[num_cols].isna().sum(axis=1) > 0,num_cols].head()
    
  # 실행 결과
  	batter_id	year	avg	G	AB	R	H	2B	3B	HR	...	SO	GDP	SLG	OBP	E	starting_salary	OPS	weight	height	weight_per_height
  0	0	2018	0.339	50	183	27	62	9	0	8	...	25	3	0.519000	0.383000	9	NaN	0.902000	93.0	1.0	93.0
  12	138	2005	0.127	39	63	9	8	2	0	0	...	15	1	0.158730	0.256757	3	NaN	0.415487	NaN	NaN	NaN
  13	138	2006	0.139	37	36	6	5	2	0	0	...	14	0	0.194444	0.326087	4	NaN	0.520531	NaN	NaN	NaN
  14	138	2007	0.000	8	4	3	0	0	0	0	...	2	1	0.000000	0.000000	0	NaN	0.000000	NaN	NaN	NaN
  15	138	2008	0.000	2	1	0	0	0	0	0	...	0	0	0.000000	0.000000	0	NaN	0.000000	NaN	NaN	NaN
  5 rows × 26 columns
  

• 주어진 데이터에서 변수 G는 선수가 뛴 경기 수를 의미함.

• 뛴 경기가 적어 성적을 산출 하지 못하는 경우에 결측치가 발생하는 것이 확인됨.

• 따라서 정규시즌과 일별 데이터, 프리시즌 데이터 모두 결측치를 0으로 대체함.

• 정규 시즌 데이터의 결측치를 0으로 대체

  # 수치형 변수에 포함되는 데이터 타입 선정
  numerics = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
    
  # 정규 시즌 데이터에서 결측치를 0으로 채우기
  regular_season_df[regular_season_df.select_dtypes(include=numerics).columns] = \
      regular_season_df[regular_season_df.select_dtypes(include=numerics).columns].fillna(0)
  regular_season_df
    
  # 실행 결과
  	batter_id	batter_name	year	team	avg	G	AB	R	H	2B	...	position	career	starting_salary	OPS	weight	height	weight_per_height	pos	hit_way	country
  0	0	가르시아	2018	LG	0.339	50	183	27	62	9	...	내야수(우투우타)	쿠바 Ciego de Avila Maximo Gomez Baez(대)	0.0	0.902	93.0	1.0	93.0	내야수	우타	foreign
  1	1	강경학	2011	한화	0.000	2	1	0	0	0	...	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000.0	0.000	72.0	1.0	72.0	내야수	좌타	korean
  2	1	강경학	2014	한화	0.221	41	86	11	19	2	...	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000.0	0.686	72.0	1.0	72.0	내야수	좌타	korean
  3	1	강경학	2015	한화	0.257	120	311	50	80	7	...	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000.0	0.673	72.0	1.0	72.0	내야수	좌타	korean
  4	1	강경학	2016	한화	0.158	46	101	16	16	3	...	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000.0	0.489	72.0	1.0	72.0	내야수	좌타	korean
  ...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
  2449	344	황진수	2014	롯데	0.000	5	5	0	0	0	...	내야수(우투양타)	석천초-대헌중-공주고	4000.0	0.000	82.0	1.0	82.0	내야수	양타	korean
  2450	344	황진수	2015	롯데	0.000	2	2	0	0	0	...	내야수(우투양타)	석천초-대헌중-공주고	4000.0	0.000	82.0	1.0	82.0	내야수	양타	korean
  2451	344	황진수	2016	롯데	0.000	11	10	2	0	0	...	내야수(우투양타)	석천초-대헌중-공주고	4000.0	0.000	82.0	1.0	82.0	내야수	양타	korean
  2452	344	황진수	2017	롯데	0.291	60	117	18	34	6	...	내야수(우투양타)	석천초-대헌중-공주고	4000.0	0.761	82.0	1.0	82.0	내야수	양타	korean
  2453	344	황진수	2018	롯데	0.167	18	24	6	4	1	...	내야수(우투양타)	석천초-대헌중-공주고	4000.0	0.564	82.0	1.0	82.0	내야수	양타	korean
  2454 rows × 35 columns
  

• 먼저 numerics라는 이름의 리스트로 수치형 변수에 해당하는 데이터 타입을 선정

• 이를 이용해 수치형 변수 중 결측치는 모두 0으로 바꿔 결측치 처리를 진행

• 일별 데이터의 결측치를 0으로 대체

  # 일별 데이터에서 결측치를 0으로 채우기
  day_by_day_df[day_by_day_df.select_dtypes(include=numerics).columns] = \
      day_by_day_df[day_by_day_df.select_dtypes(include=numerics).columns].fillna(0)
  day_by_day_df
    
  # 실행 결과
  	batter_id	batter_name	date	opposing_team	avg1	AB	R	H	2B	3B	...	RBI	SB	CS	BB	HBP	SO	GDP	avg2	year	month
  0	0	가르시아	3.24	NC	0.333	3	1	1	0	0	...	0	0	0	1	0	1	0	0.333	2018	3
  1	0	가르시아	3.25	NC	0.000	4	0	0	0	0	...	0	0	0	0	0	1	0	0.143	2018	3
  2	0	가르시아	3.27	넥센	0.200	5	0	1	0	0	...	0	0	0	0	0	0	0	0.167	2018	3
  3	0	가르시아	3.28	넥센	0.200	5	1	1	0	0	...	1	0	0	0	0	0	0	0.176	2018	3
  4	0	가르시아	3.29	넥센	0.250	4	0	1	0	0	...	3	0	0	0	0	0	1	0.190	2018	3
  ...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
  112268	344	황진수	6.23	LG	-	0	0	0	0	0	...	0	0	0	1	0	0	0	0.158	2018	6
  112269	344	황진수	6.26	넥센	0.000	1	0	0	0	0	...	0	0	0	0	0	1	0	0.150	2018	6
  112270	344	황진수	6.27	넥센	0.500	2	1	1	1	0	...	0	0	0	0	0	1	0	0.182	2018	6
  112271	344	황진수	6.28	넥센	-	0	0	0	0	0	...	0	0	0	0	0	0	0	0.182	2018	6
  112272	344	황진수	6.30	한화	0.000	2	0	0	0	0	...	0	0	0	0	0	0	0	0.167	2018	6
  112273 rows × 21 columns
  

• 같은 원리를 이용해 일별 데이터의 결측치도 처리

• 수치형 변수에 대해 결측치를 0으로 교체

• 프리시즌 데이터의 결측치를 0으로 대체

  # 프리시즌 데이터에서 결측치를 0으로 채우기
  preseason_df[preseason_df.select_dtypes(include=numerics).columns] = \
      preseason_df[preseason_df.select_dtypes(include=numerics).columns].fillna(0)
  preseason_df
    
  # 실행 결과
  	batter_id	batter_name	year	team	avg	G	AB	R	H	2B	...	SLG	OBP	E	height/weight	year_born	position	career	starting_salary	OPS	new_idx
  0	0	가르시아	2018	LG	0.350	7	20	1	7	1	...	0.550	0.409	1	177cm/93kg	1985년 04월 12일	내야수(우투우타)	쿠바 Ciego de Avila Maximo Gomez Baez(대)	NaN	0.959	가르시아2018
  1	1	강경학	2011	한화	0.000	4	2	2	0	0	...	0.000	0.500	0	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.500	강경학2011
  2	1	강경학	2014	한화	-	4	0	2	0	0	...	0.000	0.000	0	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.000	강경학2014
  3	1	강경학	2015	한화	0.130	10	23	3	3	0	...	0.130	0.286	2	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.416	강경학2015
  4	1	강경학	2016	한화	0.188	14	32	4	6	1	...	0.281	0.212	0	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.493	강경학2016
  ...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
  1388	342	황재균	2014	롯데	0.407	10	27	3	11	2	...	0.593	0.448	1	183cm/96kg	1987년 07월 28일	내야수(우투우타)	사당초-이수중-경기고-현대-우리-히어로즈-넥센-롯데-샌프란시스코	6000만원	1.041	황재균2014
  1389	342	황재균	2015	롯데	0.333	11	30	8	10	3	...	0.433	0.389	0	183cm/96kg	1987년 07월 28일	내야수(우투우타)	사당초-이수중-경기고-현대-우리-히어로즈-넥센-롯데-샌프란시스코	6000만원	0.822	황재균2015
  1390	342	황재균	2016	롯데	0.310	16	42	8	13	3	...	0.429	0.370	1	183cm/96kg	1987년 07월 28일	내야수(우투우타)	사당초-이수중-경기고-현대-우리-히어로즈-넥센-롯데-샌프란시스코	6000만원	0.799	황재균2016
  1391	342	황재균	2018	KT	0.250	6	16	3	4	1	...	0.500	0.333	3	183cm/96kg	1987년 07월 28일	내야수(우투우타)	사당초-이수중-경기고-현대-우리-히어로즈-넥센-롯데-샌프란시스코	6000만원	0.833	황재균2018
  1392	344	황진수	2014	롯데	0.000	1	1	1	0	0	...	0.000	0.000	0	181cm/82kg	1989년 02월 15일	내야수(우투양타)	석천초-대헌중-공주고	4000만원	0.000	황진수2014
  1393 rows × 30 columns
  

• 정규시즌 데이터, 일별 데이터와 같은 방식으로 프리시즌 데이터 역시 수치형 변수의 결측치 처리

• 지금까지 수치형 변수 중 결측치가 존재하는 행은 모두 0으로 대체한다는 규칙으로 3가지 데이터를 모두 동일하게 정제함.

• 다음으로 수치형 변수가 아닌 데이터의 결측치를 확인

• 수치형 변수의 결측치 처리와 마찬가지로 결측치 현황을 파악한 후 그에 따른 결측치 처리 방법을 고안

• 수치형이 아닌 변수의 결측치

  # 수치형이 아닌 변수 추출
  not_num_cols = [x for x in regular_season_df.columns if x not in num_cols]
    
  # 수치형이 아닌 변수 중 결측치가 하나라도 존재하는 행 출력
  # isna().sum(axis=1) -> 열 기준의 결측치 개수
  # df.loc[]를 통해 결측치 0개 이상 데이터를 추출
  regular_season_df.loc[regular_season_df[not_num_cols].isna().sum(axis=1) > 0,
                        not_num_cols].head()
    
  # 실행 결과
  	batter_name	team	height/weight	year_born	position	career	pos	hit_way	country
  12	백승룡	한화	NaN	1982년 08월 16일	NaN	사직초(부산극동리틀)-사직중-경남상고-경성대-한화-넥센	NaN	NaN	korean
  13	백승룡	한화	NaN	1982년 08월 16일	NaN	사직초(부산극동리틀)-사직중-경남상고-경성대-한화-넥센	NaN	NaN	korean
  14	백승룡	한화	NaN	1982년 08월 16일	NaN	사직초(부산극동리틀)-사직중-경남상고-경성대-한화-넥센	NaN	NaN	korean
  15	백승룡	한화	NaN	1982년 08월 16일	NaN	사직초(부산극동리틀)-사직중-경남상고-경성대-한화-넥센	NaN	NaN	korean
  16	백승룡	한화	NaN	1982년 08월 16일	NaN	사직초(부산극동리틀)-사직중-경남상고-경성대-한화-넥센	NaN	NaN	korean
  

• 키와 몸무게, 포지션, 초봉 등에 결측치가 존재

• 이 변수들의 결측치는 추가로 KBO사이트를 통해 데이터를 내려받거나 크롤링을 통해 데이터를 보완하면 해결할 수 있음.

• 하지만 이 변수들은 추후 분석 과정에 이용하지 않을 예정이므로 결측치 처리에서 배제함.

• 결측치 처리의 마지막 단계로 잘못된 결측 데이터를 삭제 단계

• 실제로 안타를 기록한 적이 있으나 장타율이 0인 경우, 안타와 볼넷 등을 기록한 적이 있으나 출루율이 0인 경우가 존재함.

• 해당 경우는 모두 1999〜2000년의 데이터로 삭제 처리를 진행

• 잘못된 결측 데이터를 삭제

  # 삭제할 데이터 추출
  drop_idx = regular_season_df.loc[
      # 안타가 0개 이상이면서 장타율이 0인 경우
      ((regular_season_df['H'] > 0) & (regular_season_df['SLG']==0)) |
            
      # 안타가 0개 이상 혹은 볼넷이 0개 이상 혹은 몸에 맞은 볼이 0개 이상이면서
      # 출루율이 0인 경우
      (((regular_season_df['H'] > 0) |
        (regular_season_df['BB'] > 0) |
        (regular_season_df['HBP'] > 0)) &
       (regular_season_df['OBP'] == 0))
  ].index         
    
  # 데이터 삭제
  regular_season_df = regular_season_df.drop(drop_idx).reset_index(drop=True)
  regular_season_df
  

3_2 규정 타수 정의

• 타수가 작은 선수는 출루율이나 장타율이 매우 높거나 낮게 형성될 확률이 크기 때문에 선수들의 성적을 분석하는 데 있어 규정 타수를 정의하는 것도 중요함.

• 분석에 필요 한 규정 타수를 새롭게 정의하기 위해 정규시즌 데이터를 기반으로 타수에 따른 OPS 수치 현 황을 그림으로 표현

• 타수에 따른 OPS 수치를 시각화

  plt.figure(figsize=(6, 3)) # 크기 조정
  plt.plot('AB', 'OPS', data=regular_season_df, linestyle='none', marker='o', 
           markersize=2, color='blue', alpha=0.4)
  plt.xlabel('AB', fontsize=14)
  plt.ylabel('OPS', fontsize=14)
  plt.xticks(list(range(min(regular_season_df['AB']), max(regular_season_df['AB']), 30)),
             rotation=90)
  plt.vlines(30,ymin=min(regular_season_df['OPS']),ymax=max(regular_season_df['OPS']),
             linestyles='dashed', colors='r')
  plt.show()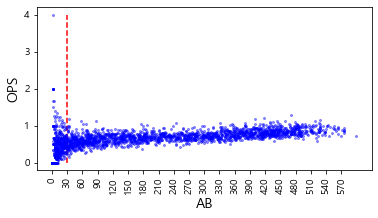
  

  

• 시각화를 통해 규정 타수에 따른 OPS 수치를 확인한 결과, 규정 타수가 적은 특정한 구간에 서 OPS가 매우 넓게 분포함을 파악할 수 있음.

• 특히 타수가 30 미만인 경우에 대해서는 OPS 분포가 매우 넓음

• 따라서, 30을 규정 타수로 정의하고 분석을 진행

• 규정 타수를 30으로 정의하는 것의 타당성을 확인하기 위해 이싱치로 판단되는 OPS를 기록한 경우를 다시 한번 탐색

• OPS 데이터의 상위 25%, 75% 수치와 그 범위를 이용해 이상치를 탐색

• 이상치를 탐색

  # OPS 이상치 탐색을 위한 수치 정의
  Q1 = regular_season_df['OPS'].quantile(0.25)
  Q3 = regular_season_df['OPS'].quantile(0.75)
  IQR = Q3 - Q1
    
  # 실제 OPS 이상치 탐색
  regular_season_df.loc[(regular_season_df['OPS'] < (Q1 - 1.5 * IQR)) |
                        (regular_season_df['OPS'] > (Q3 + 1.5 * IQR))].sort_values(
      by=['AB'], axis=0, ascending=False)[['batter_name','AB','year','OPS']].head(10)
    
  # 실행 결과
  	batter_name	AB	year	OPS
  2329	테임즈	472	2015	1.293656
  97	강정호	418	2014	1.200156
  1318	유재신	33	2018	1.192000
  416	김원섭	25	2005	0.116923
  1543	이여상	22	2013	0.090909
  681	문규현	18	2007	0.109000
  578	김회성	17	2010	0.105000
  1902	정병곤	15	2018	0.130000
  1874	정경운	15	2018	0.130000
  2384	현재윤	15	2014	1.229167
  

• 확인 결과 2015년 테임즈, 2014년 강정호처럼 성적이 매우 뛰어났던 특정 경우를 제외한다면 30타수 이하의 선수에게서 대부분 이상치가 나옴. 이를 통해 규정 타수를 30으로 정의하는 것의 타당성을 확인 가능

• 상반기 성적을 정의하기 위해 며칠까지의 기록을 상반기로 정의할 것인지 결정해야 함.

• 야구는 7월 중순쯤에 일주일 정도 휴식기를 갖음. 이 휴식 전을 상반기, 이 휴식 이후를 하반기로 봄. 따라서 이 휴식 기간에는 야구 경기 수가 다른 날짜에 비해 적을 것임.

  # 7.01~7.31 숫자 생성 후 반 올림
  major_ticks = list(np.round(np.linspace(7.01,7.31, 31),2)) 
    
  july = (day_by_day_df['date'] >= 7) & (day_by_day_df['date'] < 8) # 7월만 불러오는 index
  plt.plot(major_ticks,
           day_by_day_df['date'].loc[july].value_counts().sort_index(), marker='o')
  plt.xticks(major_ticks,rotation=90)
  plt.show()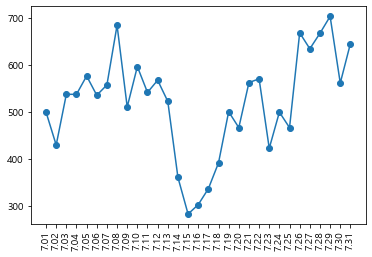
  

  

• 이것은 일별 그래프에서 7월 한 달 동안 경기를 뛴 선수들의 수의 합을 나타낸 그래프

• 다른 날짜들은 400 경기 이상의 경기 수를 기록했는데 7월14일〜7월18일은 다른 날짜와 달리 확연하게 경기 수가 적음.

• 이 시기를 휴식기라 볼 수 있으므로 2019년에도 7월 18일을 전체 시즌의 휴식기간이라고 보는 데 문제가 없음.

• 따라서 7월18일을 기준으로 상반기와 하반기로 나눔

3_3 시간변수

• 이 대회는 시기에 따른 선수들의 성적 데이터를 제공하고 있어 시계열 특성을 정확하게 파악 하는 것이 중요
• 시간 정보, 즉 시계열 정보를 반영하기 위한 방법은 많지만 이번 대회에서는 시간 변수 생성에 초점을 맞춰 문제를 해결해봄

시간 반영 함수 정의와 변수 생성

• 시간 특성을 좀 더 정확히 반영하기 위해 선수별로 과거 성적을 만들어주는 함수를 정의

• 각 선수의 1 년 전 성적, 2년 전 성적, 3년 전 성적, 4년 전 성적 등으로 다음 해의 성적을 예측하는 형식

• 주어진 데이터에서는 과거 성적이 모두 행 단위로 흩어져 있으므로 이를 통합할 데이터 프레임을 만드는 함수를 정의

• 과거 성적을 통합하는 함수

  # 시간 변수를 생성하는 함수 정의
  def lag_function(df, var_name, past):
      # df = 시간변수를 생성할 데이터 프레임
      # var_name = 시간변수 생성의 대상이 되는 변수 이름
      # past = 몇 년 전의 성적을 생성할지 결정 (정수형)
      df.reset_index(drop=True, inplace = True)
        
      #시간변수 생성
      df['lag'+str(past)+'_'+var_name] = np.nan;
      df['lag'+str(past)+'_'+'AB'] = np.nan
        
      for col in ['AB', var_name]:
          for i in range(0,(max(df.index)+1)):
              val = df.loc[(df['batter_name'] == df['batter_name'][i]) & 
                           (df['year'] == df['year'][i] - past), col]
              # 과거 기록이 결측치가 아니라면 값을 넣기
              if(len(val) != 0):
                  df.loc[i, 'lag' + str(past) + '_' + col] = val.iloc[0]
    
      #30타수 미만 결측치 처리
      df.loc[df['lag' + str(past) + '_' + 'AB'] < 30, 
             'lag' + str(past) + '_' + var_name] = np.nan
      df.drop('lag' + str(past) + '_' + 'AB', axis = 1, inplace = True)
    
      return df
  

변수 선택 & 시간 범위

• OPS는 On base Plus Slugging의 약자로 OBP(출루율)와 SLG(장타율)의 합으로 계산 (QPS= OBP+SLG)

• 따라서 각 선수의 2019년도 OPS를 예측하기 위해 OBP와 SLG를 각각 예측한 후 이를 합쳐 모델링을 진행

• 하지만 과거 성적을 통해서 수치를 예측한다고 할지라도 과거의 어떤 성적을 이용해야 할지, 과거의 성적을 얼마나 이용해야 하는지에 대한 결정이 필요함.

• 이를 확인하기 위해 상관관계를 기반으로 필요한 변수를 선택하고 기간을 설정

• 변수의 상관관계를 시각화

  # 상관관계를 탐색할 변수 선택
  numerics = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
  numeric_cols = list(regular_season_df.select_dtypes(include=numerics).drop(
      ['batter_id','year','OPS','SLG'], axis =1).columns)
  regular_season_temp = regular_season_df[numeric_cols + ['year', 'batter_name']].copy()
  regular_season_temp = regular_season_temp.loc[regular_season_temp['AB'] >= 30]
    
  # 시간변수 생성 함수를 통한 지표별 1년 전 성적 추출
  for col in numeric_cols:
      regular_season_temp = lag_function(regular_season_temp, col, 1)
    
  numeric_cols.remove('OBP')
  regular_season_temp.drop(numeric_cols, axis = 1, inplace= True)
    
  # 상관관계 도출
  corr_matrix = regular_season_temp.corr()
  corr_matrix = corr_matrix.sort_values(by = 'OBP', axis = 0, ascending=False)
  corr_matrix = corr_matrix[corr_matrix.index]
    
  # 상관관계의 시각적 표현
  f, ax = plt.subplots(figsize=(12, 12))
  corr = regular_season_temp.select_dtypes(exclude=["object","bool"]).corr()
    
  # 대각 행렬을 기준으로 한 쪽만 나타나게 설정해줍니다.
  mask = np.zeros_like(corr_matrix, dtype=np.bool)
  mask[np.triu_indices_from(mask)] = True
    
  g = sns.heatmap(corr_matrix, cmap='RdYlGn_r', vmax= 1, mask=mask, 
  center=0, annot=True, fmt='.2f', square=True, linewidths=.5, cbar_kws={"shrink": .5})
  plt.title("Diagonal Correlation HeatMap")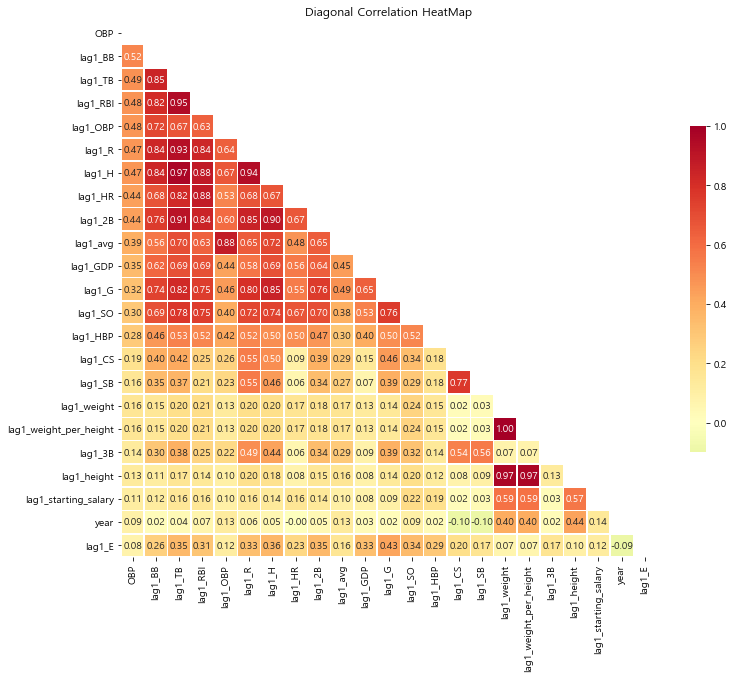
  

  

• OBP를 기준으로 확인해 본 결과, 특정 연도의 OBP(OBP)와 과거의 OBP(lag1_OBP)가 높은 상관성을 띠고 있음.

• BB(볼넷)와 같이 OBP와 높은 상관관계를 보여주는 지표가 더 존재하지만, 이들은 모두 1 년 전의 OBP와도 높은 상관관계를 보여줌.

• 독립변수 간 상관 관계가 높은 상태에서 분석을 진행할 경우 다중공선성 등의 문제가 생길 수 있으므로 BB와 같은 변수는 삭제하는 것이 타당함.

• 즉, OBP를 예측할 때는 해당 선수의 과거 OBP만을 이용하겠습니다. 직관적으로 생각하면 출루율을 예측할 때는 과거 출루율을 살펴봐야 함.

• 필요한 변수를 바탕으로 OBP 예측 모델을 위한 데이터를 먼저 구축함.

  • 우선 이 대회는 선수들의 2019년도 전체 OPS가 아니라 상반기까 지의 OPS 예측을 요구하기 때문에 상반기에 성적이 좋은 선수가 있을 수 있고 하반기에 성적이 좋은 선수가 있을 수 있음을 유추해볼 수 있음.
  • 이를 반영하기 위해 일반적으로 7월 18일까지 KBO 리그의 상반기가 진행됐던 과거 사례를 활용
  • 즉, 과거 성적을 구할 때 7월 18일까지의 성적을 이용하여 변수를 새롭게 생성
  • 하지만 날짜 정보를 가지고 있는 일별 데이터에는 희생 플라이에 대한 정보가 없으므로 추가로 평균적인 희생 플라이를 계산한 후에 과거 OBP 성적을 만들어 줌.

• 희생 플라이 계산

  #희생 플라이 구하기
  #OBP(출루율) 계산 공식 이용하여 SF(희생 플라이)계산 >> (H+BB+HBP)/OBP-(AB+BB+HBP)
  regular_season_df['SF'] = \
      regular_season_df[['H','BB','HBP']].sum(axis=1) / regular_season_df['OBP'] - \
      regular_season_df[['AB','BB','HBP']].sum(axis=1)
  regular_season_df['SF'].fillna(0, inplace = True)
  regular_season_df['SF'] = regular_season_df['SF'].apply(lambda x : round(x,0))
    
  #한 타수당 평균 희생 플라이 계산 후 필요한 것만 추출
  regular_season_df['SF_1'] = regular_season_df['SF'] / regular_season_df['AB']
  regular_season_df_SF = regular_season_df[['batter_name','year','SF_1']]
  regular_season_df_SF
    
  # 실행 결과
  	batter_name	year	SF_1
  0	가르시아	2018	0.032787
  1	강경학	2011	0.000000
  2	강경학	2014	-0.000000
  3	강경학	2015	0.009646
  4	강경학	2016	0.009901
  ...	...	...	...
  2442	황진수	2014	0.000000
  2443	황진수	2015	0.000000
  2444	황진수	2016	0.000000
  2445	황진수	2017	0.008547
  2446	황진수	2018	-0.000000
  2447 rows × 3 columns
  

• 희생 플라이 = (H+BB+HBP)/OBP- (AB+BB+HBP)라는 공식을 이용해 직접 선수별 희생 플라이를 계산

• SF_1 이라는 이름으로 타수당 평균 희생 플라이 계산 결과를 확인 가능

• 선수별 출루율

  #day_by_day에서 연도별 선수의 시즌 전반기 출루율과 관련된 성적 합 구하기
  sum_hf_yr_OBP = day_by_day_df.loc[day_by_day_df['date'] <= 7.18].groupby(
      ['batter_name','year'])['AB','H','BB','HBP'].sum().reset_index()
    
  #day_by_day와 regular season에서 구한 희생 플라이 관련 데이터를 합치기
  sum_hf_yr_OBP = sum_hf_yr_OBP.merge(regular_season_df_SF, how = 'left',
                                      on=['batter_name','year'])
    
  #선수별 전반기 희생 플라이 수 계산
  sum_hf_yr_OBP['SF'] = (sum_hf_yr_OBP['SF_1']*sum_hf_yr_OBP['AB']).apply(
      lambda x: round(x, 0))
  sum_hf_yr_OBP.drop('SF_1', axis = 1, inplace = True)
    
  #선수별 전반기 OBP(출루율) 계산
  sum_hf_yr_OBP['OBP'] = sum_hf_yr_OBP[['H', 'BB', 'HBP']].sum(axis = 1) / \
                         sum_hf_yr_OBP[['AB', 'BB', 'HBP','SF']].sum(axis = 1)
  # OBP 결측치를 0으로 처리 
  sum_hf_yr_OBP['OBP'].fillna(0, inplace = True)
    
  # 분석에 필요하지 않은 열 제거
  sum_hf_yr_OBP = sum_hf_yr_OBP[['batter_name','year','AB','OBP']]
  sum_hf_yr_OBP
    
  # 실행 결과
  C:\Users\kimminsung\AppData\Roaming\Python\Python36\site-packages\ipykernel_launcher.py:3: FutureWarning: Indexing with multiple keys (implicitly converted to a tuple of keys) will be deprecated, use a list instead.
    This is separate from the ipykernel package so we can avoid doing imports until
  batter_name	year	AB	OBP
  0	가르시아	2018	85	0.418367
  1	강경학	2011	1	0.000000
  2	강경학	2014	0	1.000000
  3	강경학	2015	156	0.342541
  4	강경학	2016	81	0.222222
  ...	...	...	...	...
  1381	황진수	2012	4	0.400000
  1382	황진수	2013	0	0.000000
  1383	황진수	2016	9	0.000000
  1384	황진수	2017	71	0.316456
  1385	황진수	2018	24	0.230769
  1386 rows × 4 columns
  

• 희생 플라이 계산을 완료했으므로 이제 선수별 OBP(출루율)를 정확히 계산할 수 있음.

• 구성한 논리대로 7월 18일까지의 성적을 추린 후 계산한 희생 플라이 데이터를 합쳐 최종 상반기 선수별 OBP를 도출

3_4 추가 변수 생성

• 이번 예측 모델링의 기본 아이디어는 한 선수의 미래 OPS(OBP, SLG)를 예측하는 데 있어 과거 해당 선수의 OPS(OBP. SLG)를 이용해 예측을 진행

• 이 과정에서 나이를 반드시 고려해야 함.

• 일반적으로 운동선수는 나이에 따라 잘하는 시기가 정해져 있는 경우가 많음

• 또한 어린 선수인지 고참 선수인지에 따라 모델이 과거 성적보다 낮게 예측 해야 하는지 높게 예측해야 하는지가 결정될 것

• 이러한 가설이 맞는지 확인하기 위해 간단하게 나이에 따른 OBP 성적 변화 추이를 시각화해 파악

• 나이에 따른 성적 변화

  # 나이 변수 생성
  regular_season_df['age'] = regular_season_df['year'] - \
                             regular_season_df['year_born'].apply(lambda x: int(x[:4]))
    
  # 나이, 평균 출루율, 출루율 중위값으로 구성된 데이터프레임 구축
  temp_df = regular_season_df.loc[regular_season_df['AB'] >= 30].groupby('age').agg(
      {'OBP':['mean','median']}).reset_index()
  temp_df.columns = temp_df.columns.droplevel()
  temp_df.columns = ['age', 'mean_OBP', 'median_OBP']
    
  # 나이에 따른 출루율 추이 시각화
  plt.figure(figsize=(12,8))
  plt.plot('age', 'mean_OBP', data=temp_df, marker='o', markerfacecolor='blue',
           markersize=12, color='skyblue', linewidth=4)
  plt.ylabel('평균OBP')
  plt.xlabel('나이')
  plt.show()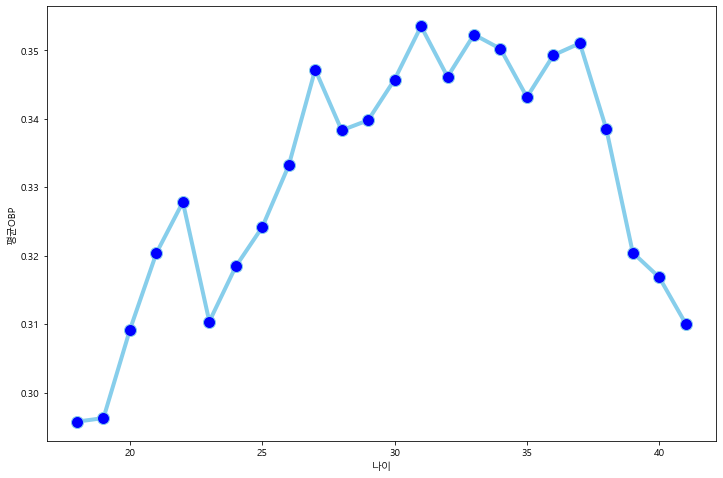
  

  

• 시각화 결과를 보니 확실히 나이에 따라 출루율의 추이가 존재

• 출루율은 20대 후반에 서 30대 초중반 사이에서 가장 높은 수치를 보여줌

• 운동선수로서의 전성기가 20대 후반 에서 30대 초중반 사이에서 형성된다고 볼 수 있음

• 또한 20대 후반에서 30대 초중반 사이의 구간 이전에는 출루율이 상승하는 경향이 있고 이후 구간에는 출루율이 하락하는 경향이 있음.

• 나이에 따라 명확하게 전성기 개념이 존재하므로 이를 반영하기 위해 나이 변수를 데이터에 추가하고 변수 생성을 완료함.

• 나이 변수 추가

  # 나이를 포함한 변수 선택
  sum_hf_yr_OBP = sum_hf_yr_OBP.merge(regular_season_df[['batter_name','year','age']],
                                      how = 'left', on=['batter_name','year'])
    
  # 총 3년 전 성적까지 변수를 생성
  sum_hf_yr_OBP = lag_function(sum_hf_yr_OBP, "OBP", 1)
  sum_hf_yr_OBP = lag_function(sum_hf_yr_OBP, "OBP", 2)
  sum_hf_yr_OBP = lag_function(sum_hf_yr_OBP, "OBP", 3)
  sum_hf_yr_OBP
    
  # 실행 결과
  	batter_name	year	AB	OBP	age	lag1_OBP	lag2_OBP	lag3_OBP
  0	가르시아	2018	85	0.418367	33	NaN	NaN	NaN
  1	강경학	2011	1	0.000000	19	NaN	NaN	NaN
  2	강경학	2014	0	1.000000	22	NaN	NaN	NaN
  3	강경학	2015	156	0.342541	23	NaN	NaN	NaN
  4	강경학	2016	81	0.222222	24	0.342541	NaN	NaN
  ...	...	...	...	...	...	...	...	...
  1381	황진수	2012	4	0.400000	23	NaN	NaN	NaN
  1382	황진수	2013	0	0.000000	24	NaN	NaN	NaN
  1383	황진수	2016	9	0.000000	27	NaN	NaN	NaN
  1384	황진수	2017	71	0.316456	28	NaN	NaN	NaN
  1385	황진수	2018	24	0.230769	29	0.316456	NaN	NaN
  1386 rows × 8 columns
  

3_5 데이터 사후 처리

• 지금까지 설명한 과정을 통해 분석에 필요한 변수를 생성했다면, 그 데이터를 바탕으로 바로 모델 생성에 들어갈 수 있는지 확인하기 위해 결측치를 다시 파악

  round(sum_hf_yr_OBP[['lag1_OBP','lag2_OBP','lag3_OBP']].isna().sum() / \
        sum_hf_yr_OBP.shape[0], 2)
  # 실행 결과
  lag1_OBP    0.41
  lag2_OBP    0.54
  lag3_OBP    0.61
  dtype: float64
  

• 확인 결과 과거 시점의 출루율에 매우 많은 결측치가 존재

• 1년 전, 2년 전, 3년 전 성적에 각각 41%, 54%, 61%의 결측치가 존재

• 변수 생성 전 결측치를 처리했으므로 이는 변수 생성 과정에서 새로 생긴 결측치라고 볼 수 있음.

• 결측치가 있는 선수가 매우 많고 또 전체 데이터의 크기가 그렇게 큰 편은 아니므로 현재 결측치를 모두 삭제하거나 0으 로 처리하는 것은 타당하지 않음

• 따라서 다음 두 가지 방식을 통해 해결

  • 선수별 출루율의 평균치를 구함.
  • 시즌별 출루율의 평균치를 구함.

• 이 두 가지를 종합해 계산한 평균 수치를 결측치 대신 삽입

• 또한 계산 과정에서 도출 되는 선수별 출루율의 평균치는 그 자체로 다시 데이터에 적용해 예측 정확도를 높이는 데 이용

• 평균 수치를 결측치 대신 삽입

  #1. 선수별 OBP 평균
  # SF = (H+BB+HBP) / OBP-(AB+BB+HBP)
  # OBP = (H+BB+HBP) / (AB+BB+HBP+SF)
  player_OBP_mean = regular_season_df.loc[regular_season_df['AB'] >= 30].groupby(
      'batter_name')['AB','H','BB','HBP','SF'].sum().reset_index()
  player_OBP_mean['mean_OBP'] = player_OBP_mean[['H', 'BB', 'HBP']].sum(axis=1) / \
                              player_OBP_mean[['AB','BB','HBP','SF']].sum(axis=1)
    
  #2. 시즌별 OBP 평균
  season_OBP_mean = regular_season_df.loc[regular_season_df['AB'] >= 30].groupby(
      'year')['AB','H','BB','HBP','SF'].sum().reset_index()
  season_OBP_mean['mean_OBP'] = season_OBP_mean[['H', 'BB', 'HBP']].sum(axis=1) / \
                                season_OBP_mean[['AB','BB','HBP','SF']].sum(axis=1)
  season_OBP_mean = season_OBP_mean[['year', 'mean_OBP']]
    
  #### player_OBP_mean(선수평균) 열 추가
  sum_hf_yr_OBP = sum_hf_yr_OBP.merge(player_OBP_mean[['batter_name', 'mean_OBP']],
                                      how ='left', on="batter_name")
  sum_hf_yr_OBP = \
      sum_hf_yr_OBP.loc[~sum_hf_yr_OBP['mean_OBP'].isna()].reset_index(drop=True)
  sum_hf_yr_OBP
    
  # 실행 결과
  batter_name	year	AB	OBP	age	lag1_OBP	lag2_OBP	lag3_OBP	mean_OBP
  0	가르시아	2018	85	0.418367	33	NaN	NaN	NaN	0.383495
  1	강경학	2011	1	0.000000	19	NaN	NaN	NaN	0.337880
  2	강경학	2014	0	1.000000	22	NaN	NaN	NaN	0.337880
  3	강경학	2015	156	0.342541	23	NaN	NaN	NaN	0.337880
  4	강경학	2016	81	0.222222	24	0.342541	NaN	NaN	0.337880
  ...	...	...	...	...	...	...	...	...	...
  1347	황진수	2012	4	0.400000	23	NaN	NaN	NaN	0.358779
  1348	황진수	2013	0	0.000000	24	NaN	NaN	NaN	0.358779
  1349	황진수	2016	9	0.000000	27	NaN	NaN	NaN	0.358779
  1350	황진수	2017	71	0.316456	28	NaN	NaN	NaN	0.358779
  1351	황진수	2018	24	0.230769	29	0.316456	NaN	NaN	0.358779
  1352 rows × 9 columns
  

• 전체 시즌을 통틀어 구한 평균 OBP가 결측치인 선수의 경우, 프로 데뷔 후 뛴 경기가 매우 적고 1, 2, 3년 전 성적이 다 결측치임

• 이런 선수들은 아예 데이터셋에서 제거

• 이제 본격적으로 시즌의 평균 성적과 선수의 평균 성적의 평균을 이용해 결측치를 처리

• 결측치를 처리하는 과정을 반복적으로 수행하므로 결측치를 처리하는 함수를 정의

• 결측치 처리 함수 정의

  # 결측치 처리하는 함수 정의
  def lag_na_fill(data_set, var_name, past, season_var_mean_data):
      # data_Set: 이용할 데이터셋
      # var_name: 시간 변수를 만들 변수 이름
      # past: 몇 년 전 변수를 만들지 결정
      # season_var_name_mean_data season별로 var_name의 평균을 구한 데이터
      
      for i in range(0,len(data_set)):
          if np.isnan(data_set["lag"+str(past)+"_"+var_name][i]):
              data_set.loc[i,["lag"+str(past)+"_"+var_name]] = (
                  data_set["mean" + "_" + var_name][i] + season_var_mean_data.loc[
                      season_var_mean_data['year'] == (data_set['year'][i] - past),
                      "mean_" + var_name].iloc[0]
                  ) / 2
      return data_set
  

• OBP 결측치 처리

  # 생성한 함수를 이용해 결측치 처리 진행
  sum_hf_yr_OBP = lag_na_fill(sum_hf_yr_OBP, "OBP", 1, season_OBP_mean) # 1년 전 성적 대체
  sum_hf_yr_OBP = lag_na_fill(sum_hf_yr_OBP, "OBP", 2, season_OBP_mean) # 2년 전 성적 대체
  sum_hf_yr_OBP = lag_na_fill(sum_hf_yr_OBP, "OBP", 3, season_OBP_mean) # 3년 전 성적 대체
  sum_hf_yr_OBP
    
  # 실행 결과
  	batter_name	year	AB	OBP	age	lag1_OBP	lag2_OBP	lag3_OBP	mean_OBP
  0	가르시아	2018	85	0.418367	33	0.369982	0.375910	0.373119	0.383495
  1	강경학	2011	1	0.000000	19	0.347434	0.348603	0.344259	0.337880
  2	강경학	2014	0	1.000000	22	0.346682	0.337511	0.343131	0.337880
  3	강경학	2015	156	0.342541	23	0.353425	0.346682	0.337511	0.337880
  4	강경학	2016	81	0.222222	24	0.342541	0.353425	0.346682	0.337880
  ...	...	...	...	...	...	...	...	...	...
  1347	황진수	2012	4	0.400000	23	0.353580	0.357883	0.359052	0.358779
  1348	황진수	2013	0	0.000000	24	0.347960	0.353580	0.357883	0.358779
  1349	황진수	2016	9	0.000000	27	0.360760	0.363874	0.357131	0.358779
  1350	황진수	2017	71	0.316456	28	0.363552	0.360760	0.363874	0.358779
  1351	황진수	2018	24	0.230769	29	0.316456	0.363552	0.360760	0.358779
  1352 rows × 9 columns
  

• 이제 분석을 위한 데이터 전처리를 완료

• 결측치를 제거해 예측 모델이 무리없이 작동하게 하고 규정 타수 선정, 시간변수 생성 등으로 예측 모델의 정확도를 높임.

3_6 SLG 데이터 전처리

• 지금까지 OBP에 대해 시간 변수 생성, 추가 변수 생성, 데이터 사후 처리 작업을 진행

• 하지만, 여기서 예측해야 하는 값은 OPS이며, OPS는 OBP(출루율)와 SLG(장타율)로 이루어짐.

• 지금부터는 OBP와 같은 논리로 SLG의 데이터 전처리를 진행

• SLG와 과거 성적 간의 상관관계를 기반으로 SLG 예측에 필요한 변수를 선택

• SLG와 과거 성적의 상관관계

  # 상관관계를 탐색할 변수 선택
  numerics = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
  numeric_cols = list(regular_season_df.select_dtypes(include=numerics).drop(
      ['batter_id','year','OPS','OBP'], axis =1).columns)
  regular_season_temp = regular_season_df[numeric_cols + ['year', 'batter_name']].copy()
  regular_season_temp = regular_season_temp.loc[regular_season_temp['AB']>=30]
    
  # 시간변수 생성 함수를 통한 지표별 1년 전 성적 추출
  for col in numeric_cols:
      regular_season_temp = lag_function(regular_season_temp, col, 1)
    
  numeric_cols.remove('SLG')
  regular_season_temp.drop(numeric_cols, axis = 1, inplace=True)
    
  # 상관관계 도출
  corr_matrix = regular_season_temp.corr()
  corr_matrix = corr_matrix.sort_values(by = 'SLG', axis = 0, ascending=False)
  corr_matrix = corr_matrix[corr_matrix.index]
    
  # 상관관계의 시각적 표현
  f, ax = plt.subplots(figsize=(12, 12))
  corr = regular_season_temp.select_dtypes(exclude=["object","bool"]).corr()
    
  # 대각 행렬을 기준으로 한쪽만 나타나게 설정해줍니다.
  mask = np.zeros_like(corr_matrix, dtype=np.bool)
  mask[np.triu_indices_from(mask)] = True
    
  cmap = sns.diverging_palette(220, 10, as_cmap=True)
  g = sns.heatmap(corr_matrix, cmap='RdYlGn_r', vmax=1, mask=mask, center=0, annot=True,
                  fmt='.2f', square=True, linewidths=.5, cbar_kws={"shrink": .5})
  plt.title("Diagonal Correlation HeatMap")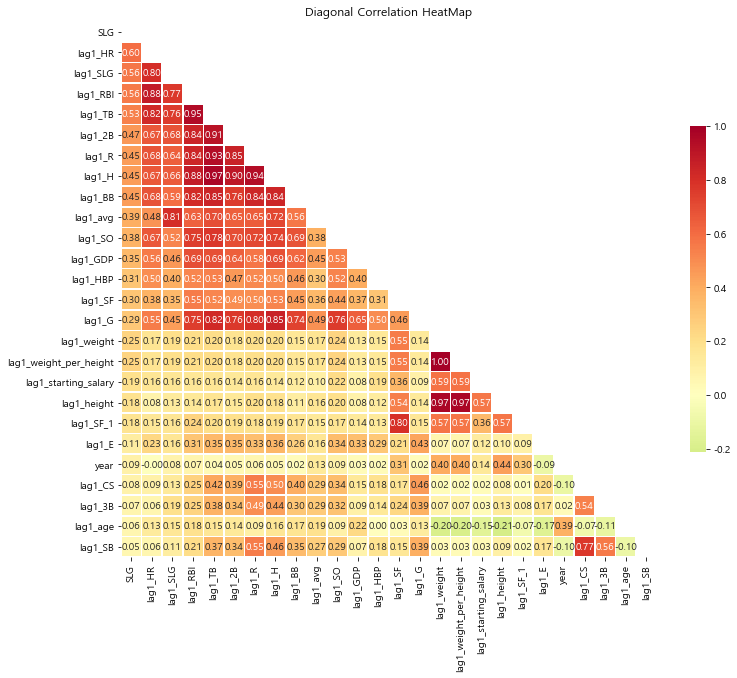
  

  

• SLG를 기준으로 확인한 결과 특정 연도의 SLG와 1 년 전 시점의 SLG(lagLSLG)가 높은 상관성을 띠고 있음.

• lag1_HR(1년 전 홈런 개수)과 같이 SLG와 높은 상관관계를 보여주는 지표가 더 존재하지만, 이들은 1년 전 SLG와 높은 상관관계를 보이기 때문에 OBP의 경우와 마찬가지로 SLG를 예측하는 데는 해당 선수의 과거 SLG만 이용

• SLG 역시 2019년도 상반기 SLG를 예측해야 하므로 7월 18일까지의 성적을 이용해 상반기 SLG를 구함.

• OBP는 희생 플라이가 없기 때문에 평균적인 희생 플라이를 계산해 상반기 OBP를 계산했다면 SLG는 주어진 데이터로 바로 계산할 수 있음.

• 상반기 SLG

  # day_by_day에서 연도별 선수의 시즌 전반기 장타율(SLG)과 관련된 성적 합 구하기
  sum_hf_yr_SLG = day_by_day_df.loc[day_by_day_df['date'] <= 7.18].groupby(
      ['batter_name','year'])['AB','H','2B','3B', 'HR'].sum().reset_index()
    
  # 전반기 장타율 계산
  sum_hf_yr_SLG['SLG'] = \
      (sum_hf_yr_SLG['H'] - sum_hf_yr_SLG[['2B', '3B', 'HR']].sum(axis=1) +
       sum_hf_yr_SLG['2B']*2 + sum_hf_yr_SLG['3B']*3 + sum_hf_yr_SLG['HR']*4
       ) / sum_hf_yr_SLG['AB']
    
  # SLG 결측치를 0으로 처리 
  sum_hf_yr_SLG['SLG'].fillna(0, inplace=True)
    
  # 필요한 칼럼만 불러오고 나이 계산
  sum_hf_yr_SLG = sum_hf_yr_SLG[['batter_name','year','AB','SLG']]
  sum_hf_yr_SLG = sum_hf_yr_SLG.merge(regular_season_df[['batter_name','year','age']],
                                      how='left', on=['batter_name','year'])
  sum_hf_yr_SLG.head()
    
  # 실행 결과
  	batter_name	year	AB	SLG	age
  0	가르시아	2018	85	0.552941	33
  1	강경학	2011	1	0.000000	19
  2	강경학	2014	0	0.000000	22
  3	강경학	2015	156	0.333333	23
  4	강경학	2016	81	0.222222	24
  

• OBP에서 발견했던 문제와 같이 SLG에서도 1, 2, 3년 전 성적을 만들어준 후 결측치가 새롭게 생기는지 확인해봄.

• 3년 전 성적까지 변수를 생성

  # 총 3년 전 성적까지 변수를 생성
  sum_hf_yr_SLG = lag_function(sum_hf_yr_SLG, "SLG", 1)
  sum_hf_yr_SLG = lag_function(sum_hf_yr_SLG, "SLG", 2)
  sum_hf_yr_SLG = lag_function(sum_hf_yr_SLG, "SLG", 3)
  display(sum_hf_yr_SLG.head())
    
  round(sum_hf_yr_SLG[['lag1_SLG', 'lag2_SLG', 'lag3_SLG']].isna().sum()/\
        sum_hf_yr_SLG.shape[0], 2)
    
  # 실행 결과
    
  batter_name	year	AB	SLG	age	lag1_SLG	lag2_SLG	lag3_SLG
  0	가르시아	2018	85	0.552941	33	NaN	NaN	NaN
  1	강경학	2011	1	0.000000	19	NaN	NaN	NaN
  2	강경학	2014	0	0.000000	22	NaN	NaN	NaN
  3	강경학	2015	156	0.333333	23	NaN	NaN	NaN
  4	강경학	2016	81	0.222222	24	0.333333	NaN	NaN
  lag1_SLG    0.41
  lag2_SLG    0.54
  lag3_SLG    0.61
  dtype: float64
  

• OBP에서 결측치를 처리할 때 선수 평균 성적을 새로운 변수로 생성

• 이후 lag_na_ fill 함수와 시즌 성적, 선수의 평균 성적을 이용해 과거 성적의 결측치를 처리했던 것처럼 SLG에서도 동일한 과정을 적용

• 과거 SLG의 결측치 처리

  # 선수별 SLG 평균 데이터(player_SLG_mean)를 만듭니다
  player_SLG_mean = regular_season_df.loc[regular_season_df['AB'] >= 30].groupby(
      'batter_name')['AB','H','2B','3B','HR'].sum().reset_index()
  player_SLG_mean['mean_SLG'] = \
      (player_SLG_mean['H'] - player_SLG_mean[['2B','3B','HR']].sum(axis = 1) +
       player_SLG_mean['2B']*2 + player_SLG_mean['3B']*3 + player_SLG_mean['HR']*4
      ) / player_SLG_mean['AB']
    
  # 시즌별 SLG 평균 데이터(season_SLG_mean)를 만듭니다
  season_SLG_mean = regular_season_df.loc[regular_season_df['AB'] >= 30].groupby(
      'year')['AB','H','2B','3B','HR'].sum().reset_index()
  season_SLG_mean['mean_SLG'] = \
      (season_SLG_mean['H'] - season_SLG_mean[['2B','3B','HR']].sum(axis = 1) + 
       season_SLG_mean['2B']*2 + season_SLG_mean['3B']*3 + season_SLG_mean['HR']*4
      ) / season_SLG_mean['AB']
    
  # 선수 평균의 SLG(player_OBP_mean)를 새로운 변수로 더합니다.
  sum_hf_yr_SLG = sum_hf_yr_SLG.merge(player_SLG_mean[['batter_name', 'mean_SLG']],
                                      how='left', on="batter_name")
    
  # 선수 평균의 성적이 결측치이면 데이터에서 제거합니다.
  sum_hf_yr_SLG = \
      sum_hf_yr_SLG.loc[~sum_hf_yr_SLG['mean_SLG'].isna()].reset_index(drop=True)
    
  # 결측치 처리
  sum_hf_yr_SLG = lag_na_fill(sum_hf_yr_SLG, "SLG", 1, season_SLG_mean) #1년전 성적 대체
  sum_hf_yr_SLG = lag_na_fill(sum_hf_yr_SLG, "SLG", 2, season_SLG_mean) #2년전 성적 대체
  sum_hf_yr_SLG = lag_na_fill(sum_hf_yr_SLG, "SLG", 3, season_SLG_mean) #3년전 성적 대체
    
  display(sum_hf_yr_SLG.head())
  round(sum_hf_yr_SLG[['lag1_SLG', 'lag2_SLG', 'lag3_SLG']].isna().sum()/\
        sum_hf_yr_SLG.shape[0], 2)
    
  # 실행 결과
  	batter_name	year	AB	SLG	age	lag1_SLG	lag2_SLG	lag3_SLG	mean_SLG
  0	가르시아	2018	85	0.552941	33	0.481855	0.481498	0.476627	0.519126
  1	강경학	2011	1	0.000000	19	0.372902	0.380882	0.361716	0.332527
  2	강경학	2014	0	0.000000	22	0.362931	0.349344	0.359616	0.332527
  3	강경학	2015	156	0.333333	23	0.389415	0.362931	0.349344	0.332527
  4	강경학	2016	81	0.222222	24	0.333333	0.389415	0.362931	0.332527
  lag1_SLG    0.0
  lag2_SLG    0.0
  lag3_SLG    0.0
  dtype: float64
  

• 확인 결과 데이터에 결측치가 더는 존재하지 않음

• 이제 변수 생성, 결측치 처리까지 필 요한 데이터 전처리를 모두 완료

• 이는 머신러닝을 이용해 KBO 타자의 2019 상반 기 시즌 성적 예측을 위한 모델링 작업을 하기 전에 필요한 준비가 모두 완료됐음을 의미

• 이후 과정에서는 전처리한 데이터를 통해 KBO 타자의 다음 시즌 OPS를 예측하기 위한 학습을 진행

4_ 모델 구축과 검증📑

• 지금까지 이번 대회의 개요를 이해하고, 탐색적 데이터 분석 및 데이터 전처리 과정을 마침
• 이 모든 과정은 모델링을 위한 선행 과정이라고 볼 수 있음.
• 여기서 모델링은 <2019 시즌 상반기 KBO 타자의 OPS 성적을 예측하기 위한 머신러닝 알고리즘 생성 과정>을 통칭 하는 용어
• 이 절에서는 학습을 위해 준비한 데이터를 기반으로 모델링 직업을 진행
• 간단한 선형 모델인 릿지(Ridge) 및 라쏘(Lasso) 회귀 모델, 트리 기반 모델의 랜덤 포레스트, 최근 머신러닝 분야에서 각광받는 부스팅 모델을 각각 구축하고 그 성능을 비교해봄.

4_1 데이터 분할

• 우선 데이터 전처리 단계에서 정의한 규정 타수인 30타수 이상의 선수들만 추출

• 이후 학습에 이용할 학습용 데이터셋, 학습 결과를 평가하는 테스트용 데이터셋으로 데이터 를 분할

• 이 대회는 과거 성적의 추세로 미래 성적을 예측해야 하는데, 이를 시계열 특성이 반영돼 있다고 말합니다.

• 이 때문에 대회 시점인 2019년 기준으로 가장 가까운 과거인 2018년의 데이터를 테스트 데이터셋으로 설정하고 2018년 이전의 데이터를 학습 데이터셋으로 설정

• 데이터 분할

  # 30타수 이상의 데이터만 학습
  sum_hf_yr_OBP= sum_hf_yr_OBP.loc[sum_hf_yr_OBP['AB']>=30]
  sum_hf_yr_SLG = sum_hf_yr_SLG.loc[sum_hf_yr_SLG['AB']>=30] 
    
  # 2018년 데이터를 test 데이터 2018년 이전은 train 데이터로 나눈다.
  OBP_train = sum_hf_yr_OBP.loc[sum_hf_yr_OBP['year'] != 2018]
  OBP_test = sum_hf_yr_OBP.loc[sum_hf_yr_OBP['year'] == 2018]
    
  SLG_train = sum_hf_yr_SLG.loc[sum_hf_yr_SLG['year'] != 2018]
  SLG_test = sum_hf_yr_SLG.loc[sum_hf_yr_SLG['year'] == 2018]
  print(OBP_train.shape, OBP_test.shape, SLG_train.shape, SLG_test.shape)
    
  # 실핼 결과
  (872, 9) (150, 9) (872, 9) (150, 9)
  

• 확인 결과 테스트용 데이터로 이용될 2018년의 데이터는 150개, 학습용 데이터로 이용될 2018년 이전의 데이터는872개 존재

• 데이터를 학습용과 테스트용으로 분할했으므로 이제 평가지표를 생성

• 평가지표를 이용해 테스트용 데이터셋에서 우수한 모델을 찾아야 함

• 대회의 평가지표에 맞게 평가하기 위해 새롭게 함수를 만듦

• WRMSE 정의

  def wrmse(v,w,p):
      # v: 실제값
      # w: 타수
      # p: 예측값
      return sum(np.sqrt(((v-p)**2 * w) / sum(w)))
  

• 대회의 평가지표인 WRMSE에 맞춰 새롭게 함수를 정의

• 이제 이 함수를 통해 앞으 로 진행할 모델링이 얼마나 잘 적용되는지를 파악할 수 있습니다, 모델 선택, 하이퍼파라미터 튜닝 등 이후 진행할 과정에서 이 함수를 기반으로 최적의 모델을 선택

4_2 모델 선택

• 데이터 분할까지 완료했으므로 이제 본격적인 학습 과정을 진행
• 학습을 위해 다양한 모델을 이용할 것이며 각 모델의 성능을 비교해 가장 좋은 성능을 보인 모델을 최종 선택하는 방법을 이용
• 여기서는 네 가지 모델의 성능을 비교하겠습니다.
  • 릿지 회귀 모델
  • 라쏘 회귀 모델
  • 랜덤 포레스트
  • XGBoos
• 선택 실습 코드는 릿지 회귀 모델 랜덤 포레스트 등 각 알고리즘의 최적 모수를 찾는 과정을 포함하므로 코드 실행 시간이 길어질 수 있음.

릿지와 라쏘

• 릿지 회귀 모델과 라쏘 회귀 모델은 모두 일반적으로 사용되는 선형회귀 모델을 변형시킨 알고리즘

• 선형회귀 모델 학습에 추가로 적절한 페널티를 부여해 더 일반화된 모델을 만들어 내는 것이 목적

• 선형회귀 모델은 최신 알고리즘보다 성능이 떨어지지만, 해석하기 쉽다는 장점이 있음

• 그리고 데이터가 적을 때 상대적으로 강점을 보이는 모델이기도 함.

• 이번 분석에서는 릿지와 라쏘 회귀 모델 모두 주어진 범위 내에서 모든 경우의 수를 비교해 최적의 모수를 결정 하는 방법인 그리드 탐색(grid search) 방법을 이용해 모델링을 진행

• 릿지와 라쏘 회귀 모델

  from sklearn.linear_model import Ridge, Lasso
  from sklearn.model_selection import GridSearchCV
    
  # log 단위(1e+01)로 1.e-04 ~ 1.e+01 사이의 구간에 대해 parameter를 탐색한다. 
  lasso_params = {'alpha':np.logspace(-4, 1, 6)} 
  ridge_params = {'alpha':np.logspace(-4, 1, 6)} 
    
  # GridSearchCV를 이용하여 dict에 Lasso, Ridege OBP 모델을 저장한다.
  OBP_linear_models = {
      'Lasso': GridSearchCV(Lasso(), param_grid=lasso_params).fit(
          OBP_train.iloc[:,-5:], OBP_train['OBP']).best_estimator_,
      'Ridge': GridSearchCV(Ridge(), param_grid=ridge_params).fit(
          OBP_train.iloc[:,-5:], OBP_train['OBP']).best_estimator_,}
    
  # GridSearchCV를 이용하여 dict에 Lasso, Ridge SLG 모델을 저장한다
  SLG_linear_models = {
      'Lasso': GridSearchCV(Lasso(), param_grid=lasso_params).fit(
          SLG_train.iloc[:,-5:], SLG_train['SLG']).best_estimator_,
      'Ridge': GridSearchCV(Ridge(),param_grid=ridge_params).fit(
          SLG_train.iloc[:,-5:], SLG_train['SLG']).best_estimator_,}
  

랜덤 포레스트

• 랜덤 포레스트는 트리 기반 모델로 보편적으로 쓰이는 알고리즘

• 랜덤 포레스트 역시 릿지와 라쏘 회귀 분석 모델과 마찬가지로 그리드 탐색을 통해 최적의 모수를 찾아 모델을 형성

• i5-8250U CPU, 메모리 12GB 환경에서 약 559초 소요됨.

• 실행환경 에 따라 아래 코드 실행에 걸리는 시간은 달라질 수 있음

• 랜덤 포레스트

  import time
  from sklearn.ensemble import RandomForestRegressor 
  start = time.time() # 시작 시간 저장
    
  # 랜덤 포레스트의 parameter 범위를 정의한다.
  RF_params = {
      'n_estimators': [50,100,150,200,300,500,1000],
      'max_features': ['auto', 'sqrt'],
      'max_depth' : [1,2,3,5,6,10],
      'min_samples_leaf': [1, 2, 4],
      'min_samples_split': [2, 3, 5, 10]}
    
  # GridSearchCV를 이용하여 dict에 OBP Randomforest 모델을 저장한다.
  OBP_RF_models = {
      'RF': GridSearchCV(
          RandomForestRegressor(random_state=42), param_grid=RF_params, n_jobs=-1
          ).fit(OBP_train.iloc[:,-5:], OBP_train['OBP']).best_estimator_}
    
  # GridSearchCV를 이용하여 dict에 OBP Randomforest 모델을 저장한다.
  SLG_RF_models = {
      'RF': GridSearchCV(
          RandomForestRegressor(random_state=42), param_grid=RF_params, n_jobs=-1
          ).fit(SLG_train.iloc[:,-5:], SLG_train['SLG']).best_estimator_}
    
  print(f"걸린시간 : {np.round(time.time() - start,3)}초") # 현재시간 – 시작시간(단위 초)
    
  # 실행 결과
  걸린시간 : 180.643초
  

XGBoost(eXtra Gradient Boost)

• XGBoost는 랜덤 포레스트와 마찬가지로 트리 기반 모델

• 특히 학습을 진행할 때 오분류된 데이터에 가중치를 부여해 성능을 높이고자 하는 모델

• 마찬가지로 그리드 탐색 방식을 이용해 XGBoost 모델을 생성

• Mac 기반의 OS를 이용하는 경우 brew install libomp 명령 등을 실행해 OpenMP 라이브 러리를 사전에 설치해두어야 함.

• XGBoost

  import xgboost as xgb 
  start = time.time() # 시작 시간 저장
    
  # xgboost parmeter space를 정의한다.
  XGB_params = {
      'min_child_weight': [1,3, 5,10],
      'gamma': [0.3,0.5, 1, 1.5, 2, 5],
      'subsample': [0.6, 0.8, 1.0],
      'colsample_bytree': [0.6, 0.8, 1.0],
      'max_depth': [3, 4, 5,7,10]}
  # GridSearchCV를 통해 parameter를 탐색하게 정의한다.
  XGB_OBP_gridsearch = GridSearchCV(xgb.XGBRegressor(random_state=42),
      param_grid=XGB_params, n_jobs=-1) 
    
  XGB_SLG_gridsearch = GridSearchCV(xgb.XGBRegressor(random_state=42),
      param_grid=XGB_params, n_jobs=-1)
    
  # 모델 학습
  XGB_OBP_gridsearch.fit(OBP_train.iloc[:,-5:], OBP_train['OBP'])
  XGB_SLG_gridsearch.fit(SLG_train.iloc[:,-5:], SLG_train['SLG'])
    
  print(f"걸린시간 : {np.round(time.time() - start,3)}초") # 현재시간 – 시작시간(단위 초)
    
  # 실행 결과
  걸린시간 : 228.336초
  

알고리즘별 성능 비교

• 지금까지 릿지 회귀 모델, 라쏘 회귀 모델, 랜덤 포레스트, XGBoost의 4가지 모델을 생성

• 이제 이 모델 중 어느 모델이 이번 대회에 최적화된 모델인지 찾아내는 작업을 진행

• 모델을 이용해 테스트 데이터셋인 2018년 데이터에 대해 예측을 진행

• 모델의 평가는 대회의 성능 평가척도인 WRMSE 값을 통해 진행

• OPS를 이 루는 두 가지 영역인 출루율(OBP)과 장타율(SLG)중 출루율을 먼저 볼 것임

• 출루율 예측 모델 성능 비교

  # 테스트 데이터셋(2018년)의 선수들의 OBP를 예측
  Lasso_OBP = OBP_linear_models['Lasso'].predict(OBP_test.iloc[:,-5:])
  Ridge_OBP = OBP_linear_models['Ridge'].predict(OBP_test.iloc[:,-5:])
  RF_OBP = OBP_RF_models['RF'].predict(OBP_test.iloc[:,-5:])
  XGB_OBP = XGB_OBP_gridsearch.predict(OBP_test.iloc[:,-5:])
    
  # test 데이터의 WRMSE 계산
  wrmse_score = [wrmse(OBP_test['OBP'], OBP_test['AB'], Lasso_OBP),
                 wrmse(OBP_test['OBP'], OBP_test['AB'], Ridge_OBP),
                 wrmse(OBP_test['OBP'], OBP_test['AB'], RF_OBP),
                 wrmse(OBP_test['OBP'], OBP_test['AB'], XGB_OBP)]
    
  x_lab = ['Lasso', 'Ridge', 'RF', 'XGB']
    
  plt.bar(x_lab, wrmse_score)
  plt.title('WRMSE of OBP', fontsize=20)
  plt.xlabel('model', fontsize=18)
  plt.ylabel('', fontsize=18)
  plt.ylim(0,0.5)
    
  # 막대그래프 위에 값을 표시해준다.
  for i, v in enumerate(wrmse_score):
      plt.text(i-0.1, v + 0.01, str(np.round(v,3))) # x 좌표, y 좌표, 텍스트를 표현한다.
        
  plt.show()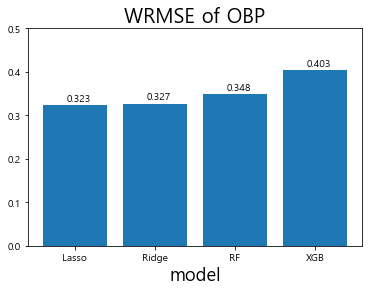
  

  

• 모델 검증 결과 라쏘 회귀 모델은 0.325, 릿지회귀 모델은 0.33, 랜덤 포레스트는 0.323. XGBoost는 0.394의 WRMSE 수치를 기록

• 대회 평가척도인 WRMSE는 숫자가 낮을수록 좋은 성능을 의미한다는 것을 기억할 것

• 출루율 예측을 위한 모델을 살펴본 결과, XGBoost가 가장 안 좋은 성능을 보여주고 있으며 랜덤 포레스트가 가장 좋은 성능을 보여줌.

• 다만, 각 모델별 성능의 구체적인 수치는 차이가 있을 수 있음.

• 대회를 진행할 당시 데이터와 현재 데이콘에서 제공되는 데이터에 다소 차이가 있기 때문

• 이번 예제에서는 대회 당시의 모델 성능을 기반으로 분석 흐름을 어떻게 가져갔는지 집중해서 살펴보겠음.

• 다음으로 장타율(SLG)을 예측하여 그 결과를 비교

• 장타율(SLG) 예측 모델 성능 비교

  # 테스트 데이터셋(2018년)의 선수들의 SLG를 예측
  Lasso_SLG = SLG_linear_models['Lasso'].predict(SLG_test.iloc[:,-5:])
  Ridge_SLG = SLG_linear_models['Ridge'].predict(SLG_test.iloc[:,-5:])
  RF_SLG = SLG_RF_models['RF'].predict(SLG_test.iloc[:,-5:])
  XGB_SLG = XGB_SLG_gridsearch.predict(SLG_test.iloc[:,-5:])
    
  # test데이터 WRMSE 계산
  wrmse_score_SLG = [wrmse(SLG_test['SLG'], SLG_test['AB'], Lasso_SLG),
                     wrmse(SLG_test['SLG'], SLG_test['AB'], Ridge_SLG), 
                     wrmse(SLG_test['SLG'], SLG_test['AB'], RF_SLG),
                     wrmse(SLG_test['SLG'], SLG_test['AB'], XGB_SLG)]
    
  x_lab = ['Lasso', 'Ridge', 'RF', 'XGB']
    
  plt.bar(x_lab, wrmse_score_SLG)
  plt.title('WRMSE of SLG', fontsize=20)
  plt.xlabel('model', fontsize=18)
  plt.ylabel('', fontsize=18)
  plt.ylim(0, 0.9)
    
  # 막대그래프 위에 값을 표시해준다.
  for i, v in enumerate(wrmse_score_SLG):
      plt.text(i-0.1, v + 0.01, str(np.round(v,3))) # x 좌표, y 좌표, 텍스트를 표현한다.
  plt.show()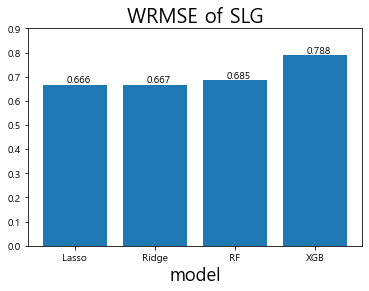
  

  

• 이렇게 해서 SLG 예측의 모델 성능을 평가

• 모델 검증 결과 라쏘 회귀 모델은 0.674, 릿지 회귀 모델은 0.677, 랜덤 포레스트는 0.7, XGBoost는 0.793의 WRMSE 수치 를 기록

• XGBoost가 가장 안 좋은 성능을 보여주고 있으며 라쏘 회귀 모델이 가장 좋은 성능을 보여줌

• 장타율 역시 출루율과 마찬가지로 모델별 구체적 수치에는 차이가 있을 수 있음

4_3 결과 해석 및 평가

랜덤 포레스트

• 앞의 단계를 통해 과거 성적을 기반으로 미래 성적을 예측하는 모델을 구축

• 모델을 구축했으므로 이제는 어떤 변수가 모델 성능에 많은 영향을 끼치는지 파악 가능

• 랜덤 포레스트와 같은 트리 기반 모델에서는 변수 중요도를 쉽게 파이썬 환경에서 도출 가능

• 각 변수의 중요도에 따라 이를 또 다시 활용할 수도 있으므로 출루율과 장타율 각각 에 대한 랜덤 포레스트 모델에서의 변수 중요도를 확인

• 랜덤 포레스트 모델에서의 변수 중요도

  plt.figure(figsize=(15,6)) # 그래프의 크기 지정
  plt.subplot(1,2,1) # 1행 2열의 첫번째(1,1) 그래프
    
  #가로막대 그래프
  plt.barh(OBP_train.iloc[:,-5:].columns,OBP_RF_models['RF'].feature_importances_) 
    
  plt.title('Feature importance of RF in OBP')
  plt.subplot(1,2,2) # 1행 2열의 두번째(1,2) 그래프
  plt.barh(SLG_train.iloc[:,-5:].columns,SLG_RF_models['RF'].feature_importances_)
  plt.title('Feature importance of RF in SLG')
  plt.show()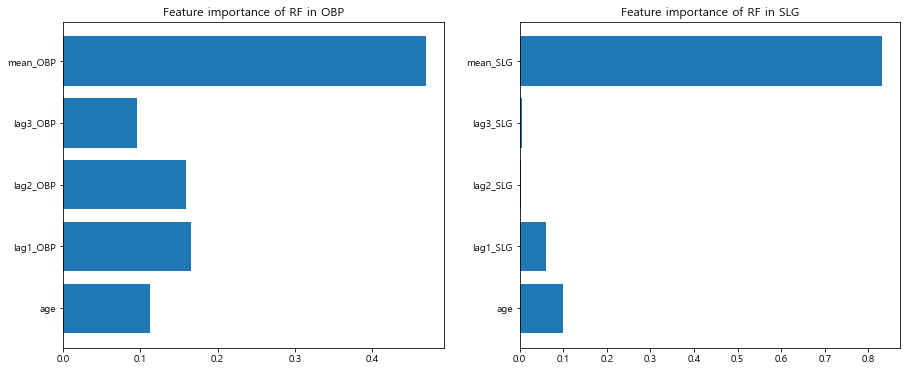
  

  

• 랜덤 포레스트의 변수 중요도를 확인한 결과 출루율과 장타율 모두 평균 기록이 가장 높은 수치를 기록

• 이는 예측 성능에 있어 평균 출루율 및 평균 장타율이 가장 크게 영향을 미친다는 것을 의미

• 그 뒤를 이어 OBP에서는 1 년 전 성적, 2년 전 성적 순서로 SLG 에서는 나이, 1 년 전 성적 순서로 높은 변수 중요도를 보임.

라쏘와 릿지 회귀 모델

• 라쏘 회귀 모델과 릿지 회귀 모델은 결과의 해석에 있어 장점이 있다고 함.

• 이번 분석 에서도 alpha 값과 계수의 값을 통해 각 변수의 중요성에 대해 해석

• 계수는 각 변수에 곱해지는 가중치를 의미하며 alpha 값은 페널티의 정도를 의미

• 라쏘 모델의 alpha 값과 선형 계수 값

  # Lasso에서 GridSearchCV로 탐색한 최적의 alpha값 출력
  print('Alpha : ', OBP_linear_models['Lasso'].alpha) 
  # Lasso model의 선형 계수 값 출력
  display(pd.DataFrame(OBP_linear_models['Lasso'].coef_.reshape(-1, 5),
                       columns=OBP_train.iloc[:,-5:].columns, index = ['coefficient']))
    
  print('Alpha : ', SLG_linear_models['Lasso'].alpha)
  display(pd.DataFrame(SLG_linear_models['Lasso'].coef_.reshape(-1, 5),
                       columns=SLG_train.iloc[:,-5:].columns, index = ['coefficient']))
    
  # 실행 결과
  Alpha :  0.0001
  age	lag1_OBP	lag2_OBP	lag3_OBP	mean_OBP
  coefficient	0.003195	0.018249	0.0	0.0	0.864913
  Alpha :  0.0001
  age	lag1_SLG	lag2_SLG	lag3_SLG	mean_SLG
  coefficient	0.0049	0.081209	0.0	-0.0	0.836453
  

• 우선 출루율에서는 평균 성적과 나이만 이용하는 것, 장타율에서는 평균 성적과 나이, 1 년 전 성적을 이용하는 것이 가장 좋은 모델이라는 결론이 도출

• 시각화를 통해 학습 과정 을 더 자세하게 봄.

• 라쏘 시각화

  from sklearn.linear_model import lars_path
  plt.figure(figsize=(15,4.8)) # 그래프 크기 지정
  plt.subplot(1,2,1) # 1행 2열의 첫 번째(1행, 1열) 그래프 
    
  # OBP 모델의 alpha 값의 변화에 따른 계수의 변화를 alpha, coefs에 저장한다.
  alphas, _, coefs = lars_path(OBP_train.iloc[:,-5:].values, OBP_train['OBP'],
                               method='lasso', verbose=True)
    
  # 피처별 alpha 값에 따른 선형 모델 계수의 절댓값의 합 
  xx = np.sum(np.abs(coefs.T), axis=1)
  # 계수의 절댓값 중 가장 큰 값으로 alpha에 따른 피처의 계수의 합을 나눈다. 
  xx /= xx[-1]
    
  plt.plot(xx, coefs.T)
  plt.xlabel('|coef| / max|coef|')
  plt.ylabel('Coefficients')
  plt.title('OBP LASSO Path')
  plt.axis('tight')
  plt.legend(OBP_train.iloc[:,-5:].columns)
    
  plt.subplot(1,2,2) # 1행 2열의 두 번째(1행, 2열) 그래프
  # SLG 모델에서 alpha 값의 변화에 따른 계수의 변화를 alpha, coefs에 저장한다.
  alphas, _, coefs = lars_path(SLG_train.iloc[:,-5:].values, SLG_train['SLG'],
                               method='lasso', verbose=True)
  xx = np.sum(np.abs(coefs.T), axis=1)
  xx /= xx[-1]
    
  plt.plot(xx, coefs.T)
  plt.xlabel('|coef| / max|coef|')
  plt.ylabel('Coefficients')
  plt.title('SLG LASSO Path')
  plt.axis('tight')
  plt.legend(OBP_train.iloc[:,-5:].columns)
  plt.show()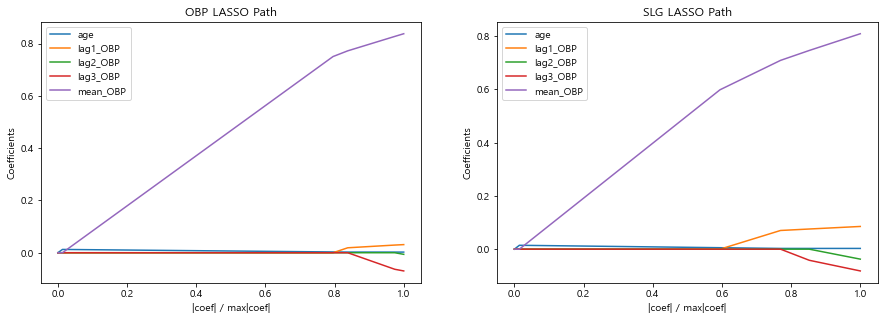
  

  

• 그래프의 왼쪽으로 갈수록 패널티 값이 커져 계수가 0으로 수렴하고 있음

• 출루율(OBP) 예측 모델에서는 1. 2, 3년 전 성적이 먼저 0으로 수렴하고 그 뒤에 나이, 그리고 한참 뒤 평 균 성적이 0으로 수렴

• SLG 모형에서는 2, 3년 전 성적이 다른 값들보다 먼저 0으로 수렴하고 그 뒤에 1년 전 성적, 나이, 평균 성적 순서로 0에 수렴

• 이를 보면 2, 3년 전 성적은 선형 모델에서 중요하게 쓰이지 않고 평균 성적이 가장 중요하게 활용