21 분 소요

image-20220408102349708

1_ 문제 정의📑

1_1 경진대회 소개

주최자 데이콘, 서울대학교 통계연구소 수원대 DS&ML 센터, 한국야구학회
총 상금 800만원
문제 유형 Time-Series（시계열）, Regression（회귀）
평가 척도 WRMSE
대회 기간 2019년 2월 8일 ~ 2019년 7월 18일
대회참여팀 219팀

표 1.1 경진대회 개요

  • 경진대회 배경

    “국내 프로야구 구단에서 데이터 사이언스 역할의 수요가 늘고 있습니다. 특히 야구에서는 특정 선수의 성적 변동성이 해마다 매우 크기 때문에 내년 성적을 예측하기 어렵습니다. 정말 못할 것이라고 생각했던 선수도 막상 내년에는 잘하고, 많은 지표가 리그 상위권이었던 선수가 내년에는 그렇지 않은 경우가 많습니다. 본 대회는 야구 데이터로 불확실성 문제를 해결하기 위해 2019년 타자들의 상반기 성적 예측을 목표로 합니다.”

    • 배경을 살펴보면 특정 선수의 성적 변동성이 해마다 매우 커서 내년의 성적을 예측하기 힘들다고 언급합니다.
    • 성적 변동성이 크다는 것은 프로야구 선수의 성적 편차가 크다는 것을 의미 합니다.
    • 결국 ‘A라는 야구선수의 내년 성적이 어떨까?’라는 질문에 구체적인 대답을 하는 것 이 매우 어렵다는 것을 의미합니다.
    • 이러한 배경을 바탕으로 야구선수의 성적 예측이라는 문 제에 대해 데이터 분석적 접근 방식의 해결방안을 요구하고 있습니다.

  • 경진대회 내용

    “2019년 타자들의 상반기 OPS를 예측하는 모델을 만들어 주세요 2010년부터 1군 엔트리에 1 번 이상 포함되었던 타자들의 역대 정규시즌, 시범경기 성적 정보를 제공합니다.”

    • 먼저 투수를 포함한 한 국 프로야구 선수 전체가 아닌 타자들만의 성적 예측을 요구합니다.
    • 두 번째로 한국 프로야구 타자들의 2019년 전체 성적이 아닌 2019년 상반기만의 성적 예측을 요구합니다.
    • 세 번째로 홈런, 안타 등 다양한 지표를 가지고 있는 타자들의 성적 중 OPS라는 수치를 예측해야 합니다.
    • 마지막으로 2019년 타자들의 상반기 OPS 성적을 역대 정규시즌과 시범경기 성적 정보를 바탕으로 예측해야 합니다.

1_2 평가 척도

  • 평가 척도 : WRMSE Weighted Root Mean Square Errorimage-20220408105038194기본적으로 실제 값과 예측값의 차이를 기준으로 평가하므로 오차가 작을수록 우수한 성능을 낼 수 있습니다.

    • 수식을 자세히 살펴보면 실제 OPS 값과 예측한 OPS 값의 오차(yi- ŷi)를 먼저 구합니다. 이후 오차를 제곱해 실제 값보다 큰 수치로 예측할 때와 작은 수치로 예측할 때 의 차이를 없애줍니다.

    • 그러고 나서 다시 오차의 제곱에 타수(wi)를 곱하고 이를 다시 모든 선수의 타수 합(Σwi)으로 나눕니다.

    • 타수의 합계는 고정된 상수이므로 이 값이 높을수록 WRMSE에 크게 영향을 미칩니다. 최종적으로는 해당 수치에 제곱근을 취하고 이를 합해 결과를 평가합니다.

  • 타자들의 OPS를 예측할 때 비주전 선수의 성적보다는 주전 선수의 성적을 예측하는 것이 더 중요할 것입니다.

  • WMSE는 이러한 경향을 반영하는 평가척도라고 볼 수 있습니다.

  • 즉 많은 타수를 기록한 선수가 적은 타수를 기록한 선수보다 WRMSE에 크게 기여합니다.

  • 한 경기에 도 타석에 들어서지 못한 선수들은 가중치가 0이므로 계산 결과도 0이 됩니다.

  • 간단한 예시 를 통해 WRMSE 값을 어떻게 산출하는지 살펴보겠습니다.

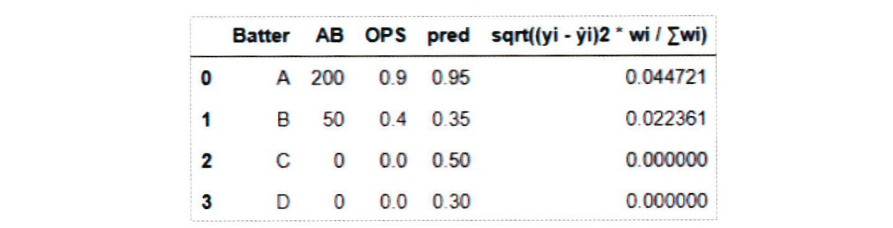
    image-20220408105103784

그림 1.2 WRMSE 평가 예시

  • 그림 1.2에서 타자(Batter) A, B의 실제 OPS(OPS)값과 예측된 OPS(pred)의 차이는 0.05 로 같습니다.
  • 그러나 맨 오른쪽 열의 값은 타자 A가 더 큽니다.
  • 이는 타자 A의 타수(AB)가 200으로 타자 B의 50보다 높기 때문입니다.
  • 그리고 타수가 0인 C, D 타자에 대해서는 어떤 값으로 예측을 하든 계산 결과가 0이 됩니다.
  • WRMSE는 숫자가 작을수록 좋은 결과라고 평가하는 척도입니다.
  • 타수가 낮은 선수의 성적이 WEMSE에 미치는 영향이 작음을 고려할 때, 경기를 많이 뛰는 선수들에 대해 예측을 잘 하는 것이 WRMSE의 값을 낮추는 데 더 중요함을 알 수 있습니다.

1_3 도메인 조사

  • 정규시즌 : 정규시즌에서의 승패 등의 성적이 쌓여 각 구 단의 최종 순위가 결정
  • 시범경기 : 정규시즌 시작 전에 열리는 비공식 경기
    • 비공식 경기이므로 최종 순위에 영향을 미치지는 않지만 경기 자체는 정규시즌과 똑같은 방식 으로 진행
    • 결국 예측 대상이 되는 타자의 OPS는 정규시즌의 성적이며 시범경기는 단순히 연습의 의미
  • 상반기 :
    • 한국 프로야구는 보통 상반기와 하반기로 나뉘 어 정규시즌이 진행
    • 상반기 이후 짧은 휴식기를 가지고 곧이어 하반기 정규시즌을 진행
    • 정확히 상반기가 몇 월 며칠까지인지는 매년 조금씩 기준이 다름
    • 2019년은 7 월 18일까지를 상반기로 정의하고 있어 분석을 진행할 때 역시 7월 18일을 상반기의 기준으로 삼음.
용어 설명
OBP 출루율(On Base Percentage). 타수 대비 아웃되지 않고 1 루로 출루한 비율
SLG 장타율(Slugging Percentage). 타수에서 기대되는 평균 루타
OPS 출루율과 장타율의 tKOn base Plus Slugging)
AB 타수(At Bat). 타자가 정규로 타격을 완료한 횟수
BB 볼넷(Base on Balls). 볼을 네 번 얻어 출루한 경우
HBP 사구(死球 Hit By Pitch). 투수가 던진 공이 타자에 맞아 출루한 경우
SF 희생 플라이(Sacrifice Fly). 타자 본인은 아웃이지만 주자를 진루시켜 준 경우
AVG 타율(Batting Average). 타수 대비I 안타 비율
IB, 2B. 3B 1루타, 2루타, 3루타, 한 번의 안타로 몇 루까지 진출했는지 표시
HR, H 홈런, 안타 (1B+2B+3B+HR)

1_4 문제 해결을 위한 접근 방식 소개

탐색적 데이터 분석 데이터 전처리 모델링 작업 추가적인 성능 향상
데이터의 현황을 면 밀하게 살펴본 후 구체적인 분석 전략을 수립 주어진 데이터를 여러 방법으로 변형 및 가공해 분석 목표에 좀 더 부합하는 데이터로 변환 머신러닝 알고리즘을 이용해 학습 및 예측을 진행하는 과정 고 이번 대회에만 적용할 수 있는 성능 향상 방법

1_5 분석 환경 구축

  • 아나콘다(Anaconda), Python3, 주피터 노트북(Jupyter Notebook)
  • 분석에 필요한 라이브러리의 목록
    • numpy : 행렬이나 대규모 다차원 배열을 처리할 수 있게 지원하는 라이브러리입니다.
    • pandas : Dataframe 형태 데이터의 조작 및 분석을 위해 파이썬 언어로 작성된 소프트웨어 라이브러리입니다.
    • seaborn : matplotlib이라는 기존 라이브러리를 기반으로 좀 더 다양한 그래프를 작성하게 해주는 라이브러리입니다.
    • sklearn : 파이썬에서 많이 쓰이는 머신러닝 기능을 제공하는 라이브러리입니다.
    • xgboost : XGBoost 모델을 불러오기 위해 사용되는 라이브러리입니다.

2_ 탐색적 데이터 분석📑

  • 탐색적 데이 터 분석을 통해 데이터의 분포 및 특성 등에 대한 정보를 파악하고 데이터 간의 관계를 확인

  • 탐색적 데이터 분석에서 양질의 정보를 얻어 이를 예측 모델링과 전처리에 활용 하기 때문

  • 시각화 로드

      from matplotlib import font_manager, rc
  import matplotlib
  import matplotlib.pyplot as plt
  import seaborn as sns
  import pandas as pd
  import numpy as np
  import platform

  if platform.system() =="Windows":
      # 윈도우인 경우 맑은 고딕 폰트를 이용
      font_name = font_manager.FontProperties(fname="c:/Windows/Fonts/malgun.ttf"
                                              ).get_name()
      rc('font', family=font_name)
  else:
      # Mac인 경우
      rc('font', family='AppleGothic')

  # 그래프에서 마이너스 기호가 표시되게 하는 설정
  matplotlib.rcParams['axes.unicode_minus'] = False

  • 프리시즌 데이터 확인

    # 프리시즌 데이터 로드
preseason_df = pd.read_csv("./data/chap01/Pre_Season_Batter.csv")
# 정규시즌 데이터 로드
regular_season_df = pd.read_csv("./data/chap01/Regular_Season_Batter.csv")
# 데이터 크기 확인
print(preseason_df.shape)
# 데이터 상단 크기 출력
display(preseason_df.head())
  
#출력 결과
(1393, 29)
batter_id	batter_name	year	team	avg	G	AB	R	H	2B	...	GDP	SLG	OBP	E	height/weight	year_born	position	career	starting_salary	OPS
0	0	가르시아	2018	LG	0.350	7	20	1	7	1	...	1	0.550	0.409	1	177cm/93kg	1985년 04월 12일	내야수(우투우타)	쿠바 Ciego de Avila Maximo Gomez Baez(대)	NaN	0.959
1	1	강경학	2011	한화	0.000	4	2	2	0	0	...	0	0.000	0.500	0	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.500
2	1	강경학	2014	한화	-	4	0	2	0	0	...	0	NaN	NaN	0	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	NaN
3	1	강경학	2015	한화	0.130	10	23	3	3	0	...	0	0.130	0.286	2	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.416
4	1	강경학	2016	한화	0.188	14	32	4	6	1	...	0	0.281	0.212	0	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.493
5 rows × 29 columns

  • 프리시즌 데이터의 기초 통계량

    # 데이터 기초 통계량 확인
display(preseason_df.describe())
  
# 출력 결과
	batter_id	year	G	AB	R	H	2B	3B	HR	TB	...	SB	CS	BB	HBP	SO	GDP	SLG	OBP	E	OPS
count	1393.000000	1393.000000	1393.000000	1393.000000	1393.000000	1393.000000	1393.000000	1393.000000	1393.000000	1393.000000	...	1393.000000	1393.000000	1393.000000	1393.000000	1393.000000	1393.000000	1364.000000	1368.000000	1393.000000	1364.000000
mean	173.434314	2013.014358	8.705671	19.201723	2.679828	5.021536	0.954774	0.119885	0.391960	7.391960	...	0.629576	0.291457	1.877961	0.330223	3.714286	0.447236	0.361012	0.317912	0.381910	0.676924
std	94.716851	4.166757	5.562686	13.395946	2.637212	4.232584	1.196904	0.379976	0.748557	6.538787	...	1.146854	0.595522	2.053392	0.642204	3.180884	0.723364	0.269892	0.151489	0.729521	0.386933
min	0.000000	2002.000000	1.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
25%	99.000000	2010.000000	6.000000	9.000000	1.000000	2.000000	0.000000	0.000000	0.000000	2.000000	...	0.000000	0.000000	0.000000	0.000000	1.000000	0.000000	0.217000	0.250000	0.000000	0.472000
50%	178.000000	2014.000000	9.000000	18.000000	2.000000	4.000000	1.000000	0.000000	0.000000	6.000000	...	0.000000	0.000000	1.000000	0.000000	3.000000	0.000000	0.344500	0.333000	0.000000	0.675000
75%	254.000000	2017.000000	11.000000	28.000000	4.000000	8.000000	2.000000	0.000000	1.000000	11.000000	...	1.000000	0.000000	3.000000	1.000000	5.000000	1.000000	0.478000	0.400000	1.000000	0.867000
max	344.000000	2018.000000	119.000000	183.000000	35.000000	51.000000	11.000000	4.000000	5.000000	68.000000	...	9.000000	4.000000	21.000000	4.000000	36.000000	5.000000	4.000000	1.000000	5.000000	5.000000
8 rows × 21 columns

  • 주어진 데이터는 1,393개의 행과 29개의 열을 가짐, 이 중에는 결측치도 포함

  • 다음으로. 연도(year)를 보면 최솟값은 2002인것으로 보아 주어진 데이터는 2002년부터의 기록임.

  • 주어진 데이터를 더 쉽게 파악하기 위해 시각화를 통해 다시 한번 데이터를 이해해보겠음.

  • 먼저, 수치형 변수에 대해 히스토그램(histogram)으로 분포를 살펴 봄.

  • 프리시즌 데이터를 히스토그램으로 시각화

    # 데이터 시각화
preseason_df.hist(figsize=(10,9))
plt.tight_layout()# 그래프간 간격 설정
plt.show()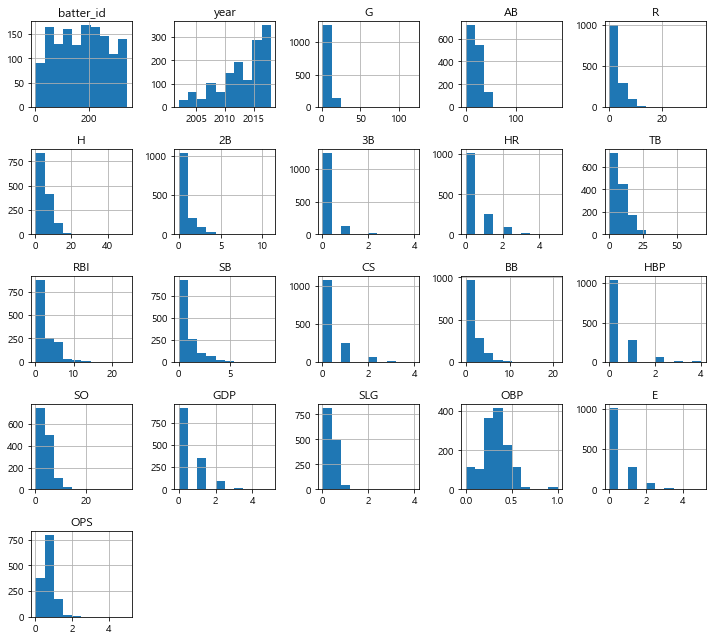

    image-20220408105126586

  • 수치형 변수의 데이터를 히스토그램으로 시각화한 결과, 2B, 3B, AB, BB, CS, SLG, R. TB 등 대부분 값이 0에 가까운 낮은 값을 기록한 것을 확인할 수 있음.

  • 이는 프리시즌의 경 기 수가 적어서 나타나는 현상이라고 추측할 수 있음.

  • 2루타(2B), 3루타(3B), HBM(사구) 등의 기록을 보면 값의 범위가 매우 작게 형성되어 있음.

  • 이 값들은 모두 0과 10 사이의 수치를 기록

  • 연도의 분포를 살펴보면 과거로 갈수록 기록의 수가 적어지는것을 확인할 수 있으며, 이는 과거의 데이터일수록 기록한 데이터 수가 적다는 것을 의미

  • 분포를 살펴본 결과 프리시즌 데이터는 그 양이 부족함.

  • 정규 시즌 데이터와 비교

    # 정규시즌 데이터에서 2002년 이후의 연도별 기록된 선수의 수
regular_count = regular_season_df.groupby('year')['batter_id'].count().rename('regular')
# 프리시즌 데이터에서 연도별 기록된 선수의 수
preseason_count = preseason_df.groupby('year')['batter_id'].count().rename('preseason')
pd.concat([regular_count, preseason_count, np.round(preseason_count/regular_count,2).rename('ratio')], axis=1).transpose().loc[:,2002:] # 2002년부터 봅니다.
  
# 실행 결과
year	2002	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018
regular	43.00	54.00	68.00	73.00	85.00	98.00	115.00	124.00	130.00	151.0	174.0	194.00	186.00	207.00	213.00	217.00	227.0
preseason	12.00	19.00	28.00	37.00	36.00	43.00	61.00	66.00	72.00	75.0	87.0	104.00	117.00	134.00	153.00	167.00	182.0
ratio	0.28	0.35	0.41	0.51	0.42	0.44	0.53	0.53	0.55	0.5	0.5	0.54	0.63	0.65	0.72	0.77	0.8

  • 표를 살펴보면 과거로 갈수록 프리시즌의 기록이 정규시즌보다 적어지는 것을 확인 가능

  • 하지만 이것은 단순히 기록의 수를 비교한 것이기 때문에 프리시즌에 존재하지만 정규시즌에 존재하지 않거나 그 반대에 해당하는 기록이 있을 수 있음.

  • 마지막으로 프리시즌의 성적과 정규시즌의 성적 간의 상관관계 도출

    • 두 데이터의 성적을 비교하기 위해서 두 데이터에 공통으로 존재하는 선수들의 기록만 사용
    • 이를 위해 선수와 연도 데이터를 이용해 새로운 열을 생성하고 새로운 열의 교집합을 이 용해 두 데이터셋에 모두 존재하는 선수만 불러오는 방식을 적용
      # 타자의 이름과 연도를 이용해 새로운 인덱스를 생성
  regular_season_df['new_idx'] = regular_season_df['batter_name'] + regular_season_df['year'].apply(str)
  preseason_df['new_idx'] = preseason_df['batter_name'] + preseason_df['year'].apply(str)
    
  # 새로운 인덱스의 교집합
  intersection_idx = list(set(regular_season_df['new_idx']).intersection(preseason_df['new_idx']))
    
  # 교집합에 존재하는 데이터만 불러오기
  regular_season_new = regular_season_df.loc[
      regular_season_df['new_idx'].apply(lambda x: x in intersection_idx)].copy()
  regular_season_new = regular_season_new.sort_values(by='new_idx').reset_index(drop=True)
    
  # 비교를 위해 인덱스로 정렬
  preseason_new = preseason_df.loc[preseason_df['new_idx'].apply(lambda x: x in intersection_idx)].copy()
  preseason_new = preseason_new.sort_values(by='new_idx').reset_index(drop=True)
    
    
  # 검정 코드
  print(regular_season_new.shape, regular_season_new.shape)
  sum(regular_season_new['new_idx'] == regular_season_new['new_idx'])
    
  # 실행 결과
  (1358, 30) (1358, 30)
  1358

  • 코딩 작업을 통한 최종 결과가 원하는 형태로 나왔는지 확인한 결과 총 1,358개의 데이터를 얻었고 그 순서도 서로 동일한 것을 확인가능

  • 최종적으로 정규시즌과 프리시즌 데이터 간의 상관관계를 도출

    # 정규시즌과 프리시즌의 상관관계 계산
  
correlation = regular_season_new['OPS'].corr(preseason_new['OPS'])
sns.scatterplot(regular_season_new['OPS'], preseason_new['OPS'])
plt.title('correlation(상관계수): '+ str(np.round(correlation, 2)), fontsize=20)
plt.xlabel("정규시즌 OPS", fontsize=12)
plt.ylabel("프리시즌 OPS", fontsize=12)
plt.show()

  • 정규시즌과 프리시즌의 성적 분포를 보면 선형적인 모습을 띠고 있지 않음.

  • 이는 정규시 즌 데이터와 프리시즌 데이터가 서로 상관성이 매우 낮다는 것을 의미

  • 탐색적 데이터 분석을 통해 알아낸 두 가지의 사실

    • 먼저, 프리시즌 데이터의 경기 기록 수는 매우 적으므로 그 구성 역시 정규시즌 데이터와는 차이가 있을 수 있다.
    • 다음으로 프리시즌 데이터와 정규시즌 데이터 간 상관관계가 매우 낮다.

  • 이를 종합했을 때 실제 분석에서는 프리시즌 데이터를 분석에서 제외

  • 이번 대회의 예측 대상은 정규시즌의 성적이기 때문에 프리시즌 데이터를 이용하지 않는 것이 더 정밀한 결과를 도출

2_2 정규시즌 데이터 분석

  • 정규시즌 데이터의 기초 통계량

    regular_season_df = pd.read_csv("./data/chap01/Regular_Season_Batter.csv")
display(regular_season_df.shape, regular_season_df.head(), regular_season_df.describe())
  
# 실행 결과
(2454, 29)
batter_id	batter_name	year	team	avg	G	AB	R	H	2B	...	GDP	SLG	OBP	E	height/weight	year_born	position	career	starting_salary	OPS
0	0	가르시아	2018	LG	0.339	50	183	27	62	9	...	3	0.519	0.383	9	177cm/93kg	1985년 04월 12일	내야수(우투우타)	쿠바 Ciego de Avila Maximo Gomez Baez(대)	NaN	0.902
1	1	강경학	2011	한화	0.000	2	1	0	0	0	...	0	0.000	0.000	1	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.000
2	1	강경학	2014	한화	0.221	41	86	11	19	2	...	1	0.349	0.337	6	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.686
3	1	강경학	2015	한화	0.257	120	311	50	80	7	...	3	0.325	0.348	15	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.673
4	1	강경학	2016	한화	0.158	46	101	16	16	3	...	5	0.257	0.232	7	180cm/72kg	1992년 08월 11일	내야수(우투좌타)	광주대성초-광주동성중-광주동성고	10000만원	0.489
5 rows × 29 columns
  
	batter_id	year	avg	G	AB	R	H	2B	3B	HR	...	SB	CS	BB	HBP	SO	GDP	SLG	OBP	E	OPS
count	2454.000000	2454.000000	2428.000000	2454.000000	2454.000000	2454.000000	2454.000000	2454.000000	2454.000000	2454.000000	...	2454.000000	2454.000000	2454.000000	2454.000000	2454.000000	2454.000000	2428.000000	2430.000000	2454.000000	2428.000000
mean	178.079462	2011.614507	0.237559	72.535045	201.514670	29.912388	55.988183	9.863488	0.957620	5.504075	...	5.290139	2.335778	20.943765	3.424613	38.596985	4.603504	0.343826	0.306684	3.676447	0.649939
std	97.557947	4.992833	0.098440	45.093871	169.537029	28.778759	52.253844	9.871314	1.647193	7.989380	...	9.088580	3.194045	21.206113	4.132614	31.801466	4.713531	0.163335	0.111778	4.585248	0.261634
min	0.000000	1993.000000	0.000000	1.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
25%	101.250000	2008.000000	0.203000	28.000000	38.250000	5.000000	8.000000	1.000000	0.000000	0.000000	...	0.000000	0.000000	3.000000	0.000000	10.000000	1.000000	0.267454	0.272727	0.000000	0.546000
50%	183.000000	2013.000000	0.255000	79.000000	163.000000	21.000000	40.000000	7.000000	0.000000	2.000000	...	2.000000	1.000000	14.000000	2.000000	33.000000	3.000000	0.360124	0.328592	2.000000	0.688637
75%	265.000000	2016.000000	0.291000	115.000000	357.500000	49.000000	100.000000	16.000000	1.000000	8.000000	...	6.000000	3.000000	34.000000	5.000000	60.000000	7.000000	0.436000	0.367000	5.000000	0.797234
max	344.000000	2018.000000	1.000000	144.000000	600.000000	135.000000	201.000000	47.000000	17.000000	53.000000	...	84.000000	21.000000	108.000000	27.000000	161.000000	24.000000	3.000000	1.000000	30.000000	4.000000
8 rows × 22 columns

  • 정규시즌 데이터는 2,454개의 행과 29개의 열을 보유

  • 연도(year)의 최솟값이 1993이므로 1993년부터의 기록을 가지고 있음.

  • 또한 앞의 프리시즌 데이터와 비교 할 때 데이터 값이 상대적으로 큰 것을 확인할 수 있음.

  • 정규시즌 데이터를 히스토그램으로 시각화

    regular_season_df.hist(figsize=(10, 9))
plt.tight_layout() # 그래프 간격 설정
plt.show()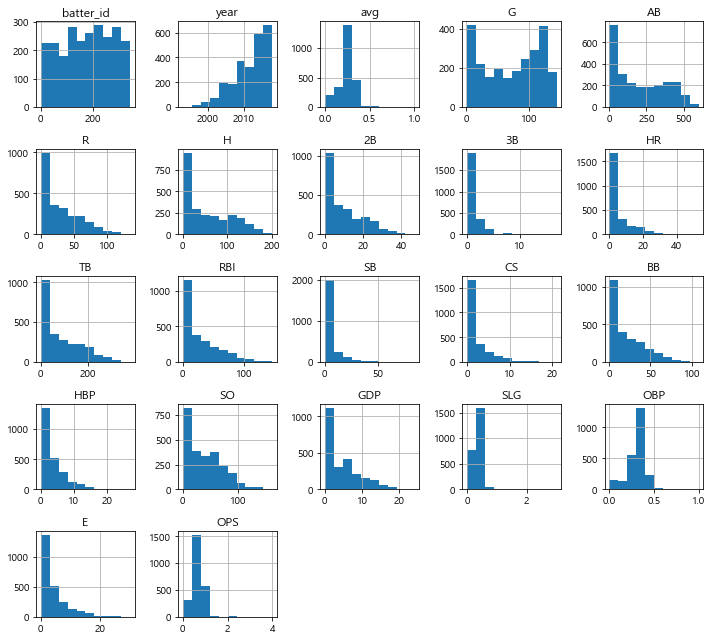

    image-20220408105134867

  • 먼저, 수치형 변수에 대해 히스토그램으로 시각화를 진행

    • 몇몇 변수가 0에 매우 치우쳐 있기는 하지만, 프리시즌 데이터와 비교했을 때 값의 범위가 더 넓어짐.
    • 또한, 값들이 상대적으로 더 오른쪽으로 퍼져 있음.
    • 이번 대회의 예측 대상인 OPS를 살펴보면 0〜4 사이의 값을 갖고 대부분의 값이 1 이하인 것을 확인할 수 있음.

  • OPS 시각화

    plt.figure(figsize=(15, 6)) # 그래프 크기 조정
plt.subplot(1,2,1) # 1행 2열의 첫번째(1행, 2열) 그래프
g = sns.boxenplot(x='year', y='OPS', data=regular_season_df, showfliers=False)
g.set_title('연도별 OPS 상자그림', size=20)
g.set_xticklabels(g.get_xticklabels(),rotation=90)
plt.subplot(1, 2, 2)
plt. plot(regular_season_df.groupby('year')['OPS']. median())
plt.title('연도별 OPS 중앙값', size=20)
plt.show()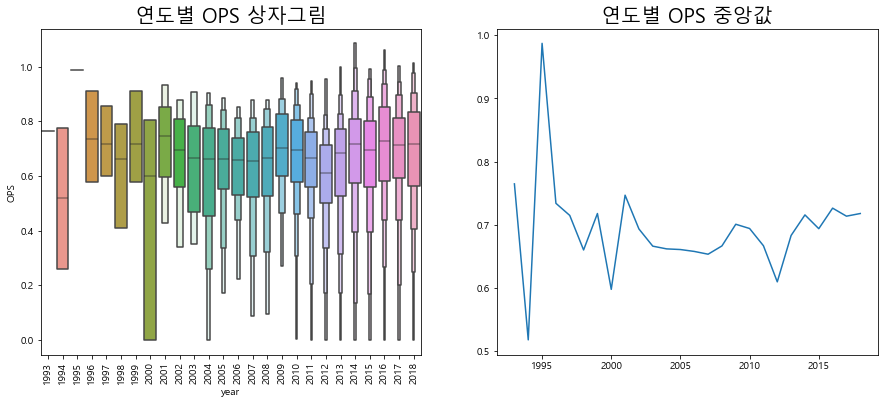

    image-20220408105140700

  • 연도별 0Ps의 분포를 상자그림을 통해 확인한 결과, 대부분 비슷한 형태를 띰

  • 하지만 연도별 중앙값을 살펴보면 2000년도를 기준으로 OPS의 변동이 차이가 있음

  • 2000년도 이전의 기록은 변동이 상당히 큰 것을 확인할 수 있고 그 이후로는 상대적으로 변동 폭이 크지 않은 추세를 보임

  • 연도별 OPS

    pd.crosstab(regular_season_df['year'], 'count').T
  
# 실행 결과
year	1993	1994	1995	1996	1997	1998	1999	2000	2001	2002	...	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018
col_0																					
count	1	2	1	7	8	10	14	20	32	43	...	124	130	151	174	194	186	207	213	217	227
1 rows × 26 columns

  • 데이터를 확인한 결과 2000년도 이전에는 기록의 수가 매우 적음.

  • 모든 연도에서 20 개 이하의 기록을 보유하고 있음.

  • 이 때문에 2000년도 이전 OPS의 변동 폭이 컸던 것임 을 유추할 수 있음.

  • 팀별 및 연도별 OPS

    # 연도별 팀의 OPS 중앙값 계산
med_OPS_team = regular_season_df.pivot_table(index=['team'], columns='year',
                                            values='OPS', aggfunc='median')
# 2005년 이후에 결측치가 존재하지 않는 팀만 확인
team_idx = med_OPS_team.loc[:,2005:].isna().sum(axis=1) <= 0
  
plt.plot(med_OPS_team.loc[team_idx,2005:].T)
plt.legend(med_OPS_team.loc[team_idx,2005:].T. columns,
            loc='center left', bbox_to_anchor=(1, 0.5)) # 그래프 범례를 그래프 밖에 위치
plt.title('팀별 성적')
plt.show()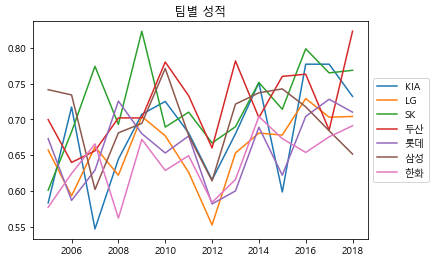

    image-20220408105146546

  • 신생팀이 아닌, 과거에 데이터를 가지고 있는 팀들을 대상으로 연도별 팀 성적을 비교해

  • 연도별 팀의 성적을 확인해 보면, 성적이 계속 달라지고 순위도 변동되는 것을 확인 가능

  • 키와 몸무게

    import re
  
regular_season_df['weight'] = regular_season_df['height/weight'].apply(
    lambda x: int(re.findall('\d+', x.split('/')[1])[0]) if pd.notnull(x) else x)
  
regular_season_df['height'] = regular_season_df['height/weight'].apply(
    lambda x: int(re.findall('\d', x.split('/')[0])[0]) if pd.notnull(x) else x)
print(regular_season_df['height/weight'][0], regular_season_df['height'][0],
regular_season_df['weight'][0])
  
# 실행 결과
177cm/93kg 1.0 93.0

  • 키와 몸무게를 분리해낸 다음 몸무게를 키로 나눠 새로운 변수를 만듦.

  • 이 값이 크면 그만큼 키에 비해 몸무게가 많이 나간다고 볼 수 있음.

  • 일반적으로 키에 비해 몸무게가 크다면 힘이 셀 것이며 반대의 경우에는 스피드가 빠를 것이라고 추측할 수 있음.

  • 따라서 계산한 값이 크다면 힘과 연관성이 높은 장타율과의 상관관계를 보고, 값이 작을 때는 스피드 가 중시 되는 출루율과의 상관관계를 확인

  • 체격과 장타율(SLG) - 출루율(OBP)의 상관관계

    # 몸무게/키 계산
regular_season_df['weight_per_height'] = regular_season_df['weight'] / \
                                         regular_season_df['height']
plt.figure(figsize=(15, 5)) # 그래프 크기 조정
plt.subplot(1, 2, 1) # 1행 2열의 첫번째(1행, 1열) 그래프
  
# 정규시즌과 프리시즌의 상관관계 계산
correlation = regular_season_df['weight_per_height'].corr(regular_season_df['OBP'])
sns.scatterplot(regular_season_df['weight_per_height'], regular_season_df['OBP'])
plt.title("'몸무게/키'와 OBP correlation(상관관계): " + str(np.round(correlation, 2)), \
          fontsize=15)
plt.ylabel('정규시즌 OBP',fontsize=12)
plt.xlabel('몸무게/키', fontsize=12)
plt.subplot(1, 2, 2)
  
# 정규시즌과 프리시즌의 상관관계 계산
correlation = regular_season_df['weight_per_height'].corr(regular_season_df['SLG'])
sns.scatterplot(regular_season_df['weight_per_height'], regular_season_df['SLG'])
plt.title("'몸무게/키'와 SLG correlation(상관관계): " + str(np.round(correlation, 2)), \
          fontsize=15)
plt.ylabel('정규시즌 SLG', fontsize=12)
plt.xlabel('몸무게/키', fontsize=12)
plt.show()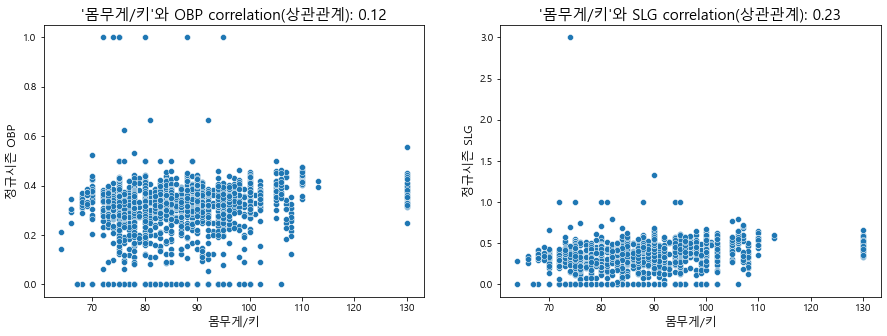

    image-20220408105155464

  • 확인 결과, 데이터는 선형적인 모습을 띠지 않으며, 그 분포가 매우 고르게 분포돼 있음을 알 수 있음

  • 이는 몸무게 및 키가 장타율과 출루율에 큰 영향을 끼치지 않음을 의미

  • 포지션

    regular_season_df['position'].value_counts()
  
# 실행 결과
내야수(우투우타)    643
외야수(우투우타)    230
외야수(좌투좌타)    201
포수(우투우타)     189
외야수(우투좌타)    184
내야수(우투좌타)    141
내야수(좌투좌타)     36
포수(우투좌타)      14
외야수(우투양타)      7
내야수(우투양타)      7
Name: position, dtype: int64

  • 내야수, 외야수 등 수비 포지션을 의미하는 단어와 우투우타, 좌투좌타 등 타자가 주로 이용하는 손을 의미하는 단어가 섞여 있음

  • 데이터를 더 자세하게 이해하기 위해 이 둘을 분리

    # position
regular_season_df['pos']=regular_season_df['position'].apply(
    lambda x: x.split('(')[0] if pd.notnull(x) else x)
  
# 우타, 좌타, 양타
regular_season_df['hit_way'] = regular_season_df['position'].apply(
    lambda x: x[-3:-1] if pd.notnull(x) else x)
print(regular_season_df['position'][0], regular_season_df['pos'][0], 
      regular_season_df['hit_way'][0])
# 실행 결과
내야수(우투우타) 내야수 우타

  • 코드 작업을 통해서 타자가 왼손잡이인지 오른손집이인지, 수비 포지션은 어디인지를 구분

  • 포지션별 OPS와 타석 방향별 OPS

    plt.figure(figsize=(15,5)) # 그래프 크기 조정
plt.subplot(1,2,1) # 1행 2열의 첫번째(1행, 1열) 그래프
ax = sns.boxplot(x='pos', y='OPS', data = regular_season_df, showfliers=False)
  
# position 별 OPS 중앙값
medians = regular_season_df.groupby(['pos'])['OPS'].median().to_dict()
  
# position별 관측치 수
nobs = regular_season_df['pos'].value_counts().to_dict()
  
# 키 값을 'n: 값' 형식으로 변환
for key in nobs: nobs[key] = "n: " + str(nobs[key])
  
# 그래프의 Xticks text 값 얻기
xticks_labels = [item.get_text() for item in ax.get_xticklabels()]
  
# tick은 tick의 위치, label은 그에 해당하는 text 값
for label in ax.get_xticklabels():
    ax.text(xticks_labels.index(label.get_text()), 
            medians[label.get_text()] + 0.03, nobs[label.get_text()],
            horizontalalignment='center', size='large', color='w', weight='semibold')
      
ax.set_title('포지션별 OPS')
  
plt.subplot(1,2,2) # 1행 2열의 두 번째(1행, 2열) 그래프
ax = sns.boxplot(x='hit_way', y='OPS', data = regular_season_df, showfliers=False)
  
# 타자 방향별 OPS 중앙값
medians = regular_season_df.groupby(['hit_way'])['OPS'].median().to_dict()
# 타자 방향 관측치 수
nobs = regular_season_df['hit_way'].value_counts().to_dict()
# 키 값을 'n: 값' 형식으로 변환
for key in nobs: nobs[key] = "n: " + str(nobs[key])
  
# 그래프의 Xticks text 값 얻기
xticks_labels = [item.get_text() for item in ax.get_xticklabels()]
  
# tick은 tick의 위치, label은 그에 해당하는 text 값
for label in ax.get_xticklabels():
    ax.text(xticks_labels.index(label.get_text()), medians[label.get_text()] + 0.03,
            nobs[label.get_text()], horizontalalignment='center', size='large',
            color='w', weight='semibold')
ax.set_title('타석방향별 OPS')
  
plt.show()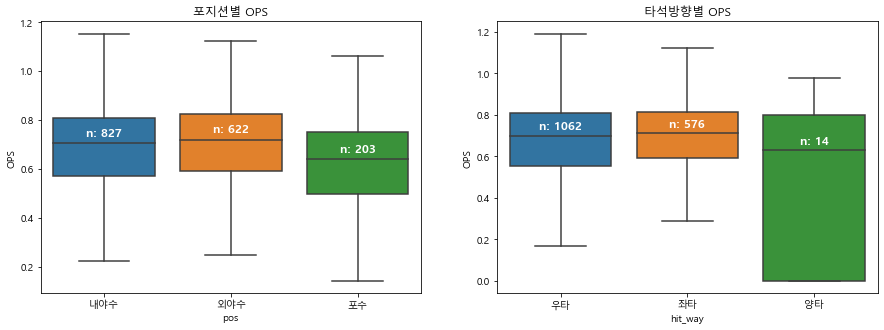

    image-20220408105201885

  • 포지션별로 OPS 값을 살펴본 결과, 내야수와 외야수의 성적은 큰 차이가 없음

    • 하지만 포수의 OPS는 다른 포지션보다 수치가 다소 작은 편
    • 즉, 포수를 제외하고 OPS 성적 에는 포지션의 영향이 그리 크지 않다는 것을 의미
    • 또한 타자가 왼손잡이인지, 오른손 잡이인지에 따른 OPS 값은 큰 차이가 없음.
    • 양손잡이의 OPS가 다소 낮은 경향은 있으 나, 그 관측치가 13개밖에 되지 않아 이 결과를 신뢰하기는 힘들 것

  • 외국인과 내국인 구분

    regular_season_df['career'].head()
  
# 실행 결과
0    쿠바 Ciego de Avila Maximo Gomez Baez(대)
1                         광주대성초-광주동성중-광주동성고
2                         광주대성초-광주동성중-광주동성고
3                         광주대성초-광주동성중-광주동성고
4                         광주대성초-광주동성중-광주동성고
Name: career, dtype: object

  • 주어진 데이터에서 career라고 표시된 값을 보면 한국인은 초등학교, 중학교, 고등학교에 대한 정보를 보유하고 있으며 외국인은 국가와 대학 순서로 정보를 보유하고 있음.

  • 한국인 의 경우 각 학교의 이름을 ‘-‘로 구분하고 있으나 외국인은 이러한 형식을 띠고 있지 않음.

  • 따라서 ‘-‘를 공백으로 대체하고 공백을 기준으로 데이터를 나눔.

  • 이를 바탕으로 career 정보를 세분화해 데이터를 재구성해 탐색

    # career를 split
foreign_country = regular_season_df['career'].apply(
    lambda x: x.replace('-', ' ').split(' ')[0])
  
# 외국만 추출
foreign_country_list = list(set(foreign_country.apply(
    lambda x: np.nan if '초' in x else x)))
  
# 결측치 처리
foreign_country_list = [x for x in foreign_country_list if str(x) != 'nan']
foreign_country_list
  
# 실행 결과
['캐나다', '쿠바', '도미니카', '네덜란드', '미국']

  • 도미니카, 미국, 쿠바, 네덜란드, 캐나다 국적을 가진 선수가 명단에 있음.

  • 해당하는 5개 국가의 국적에 속하는 선수들은 외국인으로 구분

  • 국적을 의미하는 변수 추가

    regular_season_df['country'] = foreign_country
regular_season_df['country'] = regular_season_df['country'].apply(
    lambda x: x if pd.isnull(x)
                 else ('foreign' if x in foreign_country_list else 'korean'))
regular_season_df[['country']].head()
  
# 실행 결과
  
country
0	foreign
1	korean
2	korean
3	korean
4	korean

  • 선수의 국적을 의미하는 변수를 추가

  • 외국인과 내국인 선수 성적 비교

    plt.figure(figsize=(15,5)) # 그래프 크기 조정
ax = sns.boxplot(x='country', y='OPS', data = regular_season_df, showfliers=False)
  
# 내외국인 별 OPS 중앙값 dict
medians = regular_season_df.groupby(['country'])['OPS'].median().to_dict()
# 내외국인 관측치 수 dict
nobs = regular_season_df['country'].value_counts().to_dict()
# 키 값을 'n: 값' 형식으로 변환 
for key in nobs: nobs[key] = "n: " + str(nobs[key])
  
# 그래프의 Xticks text 값 얻기
xticks_labels = [item.get_text() for item in ax.get_xticklabels()]
      
for label in ax.get_xticklabels(): # tick은 tick의 위치, label은 그에 해당하는 text 값 
    ax.text(xticks_labels.index(label.get_text()), medians[label.get_text()] + 0.03, \
            nobs[label.get_text()], # x 좌표, y 좌표, 해당 text
            horizontalalignment='center', size='large', color='w', weight='semibold') 
ax.set_title('국적별 OPS')
plt.show()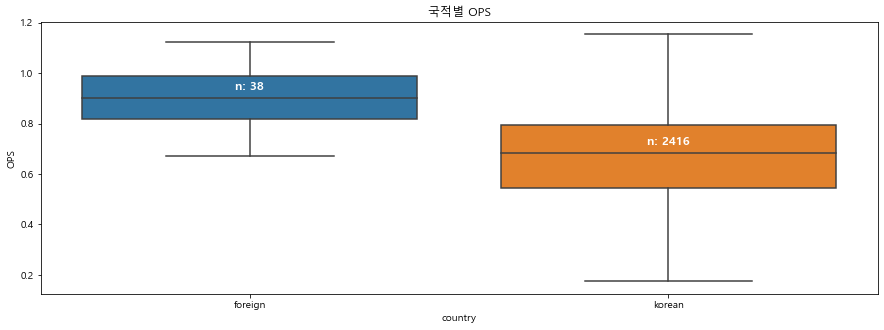

    image-20220408105208477

  • 비교 결과 외국인 선수들이 평균적으로 내국인 선수들보다 OPS 성적이 좋은 경향을 보임

  • 비록 외국인 선수의 숫자는 많지 않지만, 명확한 차이가 있음

  • 첫 연봉

    regular_season_df['starting_salary'].value_counts()
  
# 실행 결과
Output exceeds the size limit. Open the full output data in a text editor
10000만원     177
6000만원      117
3000만원      105
9000만원       97
5000만원       91
8000만원       89
30000만원      74
4000만원       62
12000만원      62
18000만원      54
7000만원       53
11000만원      49
13000만원      48
20000만원      46
25000만원      45
15000만원      41
16000만원      28
14000만원      26
28000만원      20
43000만원      17
45000만원      16
27000만원      15
21000만원      13
23000만원      12
6500만원       10
...
100000달러      4
300000달러      3
50000달러       2
17000만원       1
Name: starting_salary, dtype: int64

  • 첫 연봉의 단위가 ‘달러’와 만원’이 혼재해 있음.

  • 달러로 연봉을 받았다면 외국인이라고 생각할 수 있으며 외국인은 바로 전 단계에서 성적을 확인했으므로 만 원 단위를 가진 첫 연 봉의 데이터만 살펴봄.

  • 초봉과 성적의 상관관계

    # 결측치라면 그대로 0으로 두고 ‘만원’이 포함되어 있다면 숫자만 뽑아서 초봉으로 넣어준다. 그외 만 원 단위가 아닌 초봉은 결측치로 처리한다.
regular_season_df['starting_salary'] = regular_season_df['starting_salary'].apply(
    lambda x: x if pd.isnull(x)
                 else(int(re.findall('\d+',x)[0]) if '만원' in x else np.nan))
  
plt.figure(figsize=(15,5)) # 그래프 크기 조정
plt.subplot(1,2,1) # 1행 2열의 첫 번째(1행, 1열) 그래프
b=sns.distplot(regular_season_df['starting_salary']. \
               loc[regular_season_df['starting_salary'].notnull()], hist=True)
b.set_xlabel("starting salary",fontsize=12)
b.set_title('초봉의 분포', fontsize=20)
  
plt.subplot(1,2,2) # 1행 2열의 두 번째(1행, 2열) 그래프
  
# 정규시즌과 프리시즌의 상관관계 계산
correlation = regular_season_df['starting_salary'].corr(regular_season_df['OPS'])
b = sns.scatterplot(regular_season_df['starting_salary'], regular_season_df['OPS'])
b.axes.set_title('correlation(상관계수): '+str(np.round(correlation,2)), fontsize=20)
b.set_ylabel("정규시즌 OPS",fontsize=12)
b.set_xlabel("초봉",fontsize=12)
plt.show()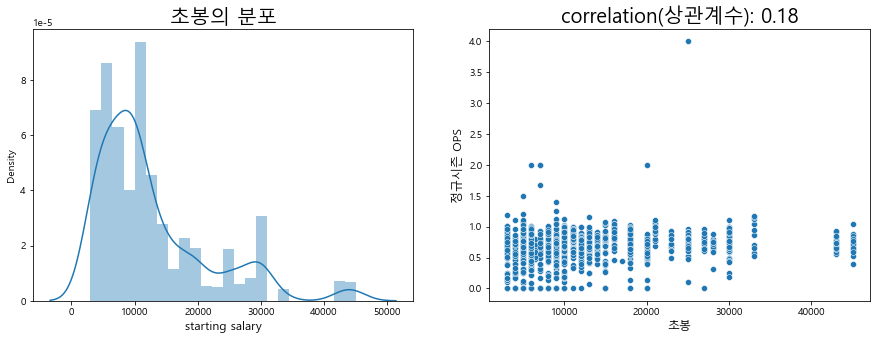

    image-20220408105213840

  • 확인 결과 첫 연봉과 성적은 큰 상관성을 보이지 않음

  • 첫 연봉에 따른 성적은 왼쪽으로 약간 치우친 정규분포 형태를 보이고 상관관계는 0.18에 그침.

  • 정규시즌 데이터를 탐색한 결과 종합

    • 먼저 OPS 성적과 높은 연관성을 띠는 주어진 데이터에서의 변수가 매우 부족합니다. 외국인 선수 OPS가 다소 높은 경향은 있으나, 외국인 선수는 매해 명단이 달라지며 그 숫자도 매우 부족해 분석에 적용하기에는 한계가 있습니다.
    • 정규시즌의 탐색적 데이터 분석 결과, 주어진 데이터를 그대로 활용하는 것이 아니라 조금 다른 차원에서의 접근이 필요한 상황임을 알 수 있습니다.

2_3 일별 데이터 분석

  • 일별 데이터

    day_by_day_df = pd.read_csv(
    './data/chap01/Regular_Season_Batter_Day_by_Day_b4.csv')
display(day_by_day_df.shape, day_by_day_df.head())
  
# 실행 결과
(112273, 20)
batter_id	batter_name	date	opposing_team	avg1	AB	R	H	2B	3B	HR	RBI	SB	CS	BB	HBP	SO	GDP	avg2	year
0	0	가르시아	3.24	NC	0.333	3	1	1	0	0	0	0	0	0	1	0	1	0	0.333	2018
1	0	가르시아	3.25	NC	0.000	4	0	0	0	0	0	0	0	0	0	0	1	0	0.143	2018
2	0	가르시아	3.27	넥센	0.200	5	0	1	0	0	0	0	0	0	0	0	0	0	0.167	2018
3	0	가르시아	3.28	넥센	0.200	5	1	1	0	0	0	1	0	0	0	0	0	0	0.176	2018
4	0	가르시아	3.29	넥센	0.250	4	0	1	0	0	0	3	0	0	0	0	0	1	0.190	2018

  • 일별 데이터를 확인해보니 연도는 정확히 표시돼 있지만, 날짜는 월과 일이 함께 표시되어 있음.

  • 주어진 데이터에서 date라는 이름의 변수를 이용해야 정확한 월 및 일 변수를 추가 가능

  • 연도별, 월별 데이터 현황

    # 날짜(date)를 ‘.’을 기준으로 나누고 첫 번째 값을 월(month)로 지정 
day_by_day_df['month'] = day_by_day_df['date'].apply(lambda x: str(x).split('.')[0])
  
# 각 연도의 월별 평균 누적 타율(avg2) 계산
agg_df = day_by_day_df.groupby(['year','month'])['avg2'].mean().reset_index()
  
# pivot_table을 이용해 데이터 변형
agg_df = agg_df.pivot_table(index=['month'], columns='year', values = 'avg2')
agg_df
  
# 실행 결과
year	2001	2002	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018
month																		
10	0.356400	0.269065	0.216583	0.203636	NaN	0.260985	0.249888	0.249638	0.033333	NaN	0.243526	0.246949	0.257841	0.273537	0.274042	0.282547	0.280289	0.277482
3	NaN	NaN	NaN	NaN	NaN	0.261714	0.261714	0.271982	NaN	0.239861	NaN	NaN	0.231236	0.210598	0.214485	0.257857	0.161979	0.238015
4	0.205217	0.319792	0.250296	0.259663	0.235317	0.267106	0.215703	0.261531	0.252546	0.262953	0.247133	0.234199	0.267994	0.259918	0.255175	0.266711	0.259430	0.263953
5	0.297157	0.267990	0.241491	0.237954	0.253527	0.264283	0.237329	0.262535	0.280842	0.272934	0.250877	0.247844	0.268355	0.273899	0.261307	0.275240	0.274374	0.274083
6	0.306926	0.275867	0.252290	0.248800	0.249913	0.264392	0.260600	0.270766	0.278781	0.274791	0.263264	0.254577	0.270533	0.283480	0.268999	0.276307	0.279060	0.280630
7	0.293171	0.266650	0.244230	0.251973	0.256396	0.262464	0.259171	0.264870	0.275054	0.265501	0.264829	0.261513	0.262812	0.275677	0.272685	0.283192	0.284565	0.280817
8	0.303489	0.270481	0.252319	0.249460	0.243570	0.265369	0.270258	0.265173	0.271796	0.271075	0.262048	0.258069	0.268122	0.282025	0.272377	0.283105	0.283283	0.283923
9	0.308636	0.248333	0.243780	0.203953	0.237058	0.258794	0.251022	0.252942	0.264468	0.265312	0.258500	0.251232	0.260571	0.272411	0.271629	0.276513	0.273213	0.277841

  • 월을 계산한 이후 연도별, 월별 데이터 현황을 간단하게 살펴봄.

  • 그 결과 결측치가 존 재하는 것이 가장 눈에 띔

  • 결측치가 존재하는 구간을 자세히 보면 3월과 10월에만 결측 치가 존재

    • 이는 연도마다 시즌의 시작일과 종료일이 다르기 때문에 발생한다고 추측 가능

  • 연도별 평균 타율

    display(agg_df.iloc[2:, 10:])
plt.plot(agg_df.iloc[2:,10:], marker = 'o', markersize=4) # 2011~2018년 데이터만 이용
plt.grid(axis='y', linestyle='-', alpha=0.4)
plt.legend(agg_df.iloc[2:,10:].columns,
           loc='center left', bbox_to_anchor=(1, 0.5)) # 범례 그래프 밖에 위치
plt.title('연도별 월 평균 타율')
plt.show()
  
# 실행 결과
year	2011	2012	2013	2014	2015	2016	2017	2018
month								
4	0.247133	0.234199	0.267994	0.259918	0.255175	0.266711	0.259430	0.263953
5	0.250877	0.247844	0.268355	0.273899	0.261307	0.275240	0.274374	0.274083
6	0.263264	0.254577	0.270533	0.283480	0.268999	0.276307	0.279060	0.280630
7	0.264829	0.261513	0.262812	0.275677	0.272685	0.283192	0.284565	0.280817
8	0.262048	0.258069	0.268122	0.282025	0.272377	0.283105	0.283283	0.283923
9	0.258500	0.251232	0.260571	0.272411	0.271629	0.276513	0.273213	0.277841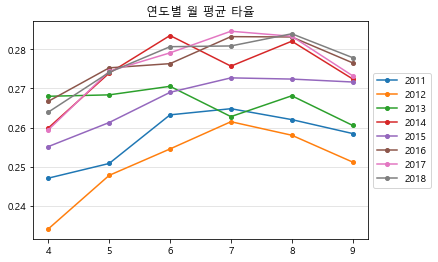

    image-20220408105222959

  • 각 연도의 월별 성적 변화를 확인해 보면 확실한 추세가 보임.

  • 시즌 시작 직후에는 대부 분 성적이 높지 않지만, 5~6월에는 되어서는 어느 정도 안정화되고 있음.

  • 이 대회가 상 반기까지의 성적을 예측하는 대회라는 것을 고려하면 모델링에 있어 매우 중요한 단서가 될 수 있는 정보임

2_4 탐색적 데이터 분석 요약

  • 탐색적 데이터 분석 단계에서는 크게 3가지 데이터를 탐색함.
    • 먼저, 프리시즌 데이터 는 데이터양에 있어 충분하지 못한 측면이 있음. 또한 정규시즌에 있는 선수의 기록이 프리시즌에 존재하지 않는 경우도 있었음.
    • 결정적으로 프리시즌 데이터와 정규시즌 데이터 간에 상관성이 매우 낮으므로 프리시즌 데이터는 사용하지 않도록 함.
    • 다음으로, 정규시즌 데이터에서 OPS가 외국인 여부에 따라 다르게 분포함을 파악함.
    • 또한 정규시즌의 일별 데이터에서 연도별 월별 선수들의 누적 성적의 변화를 살펴봄.
    • 그 결과 OPS 성적의 평균이 월별로 달라지고 7월 이후에 성적이 수렴되는 것을 확인 가능
  • 이러한 결론을 바탕으로 데이터 전처리를 진행하겠습니다

댓글남기기

참고

시간복잡도(time complexity)는 어떻게 계산하는가?

5 분 소요

코딩테스트를 준비하면서 어렵다고 느낀 부분은 효율성 검증에서 막혀 통과가 되지 않을때였습니다. 그럴때 고려해야 하는 것이 시간복잡도(time complexity)입니다. 이번 포스팅에서는 시간복잡도에 대해서 알아보고자 합니다.